Question

已知等腰△ABC中，AD⊥BC于点D，且AD=

1

2

BC，则△ABC底角的度数为（　　）

A．45°	B．75°
C．45°或15°或75°	D．60°

Answer 1

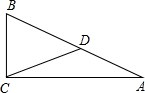
①如图1，点A是顶点时，∵AB=AC，AD⊥BC，
∴BD=CD，
∵AD=

1

2

BC，
∴AD=BD=CD，
在Rt△ABD中，∠B=∠BAD=

1

2

（180°-90°）=45°；
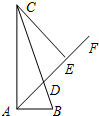
②如图2，点A是底角顶点，且AD在△ABC外部时，
∵AD=

1

2

BC，AC=BC，
∴AD=

1

2

AC，
∴∠ACD=30°，
∴∠BAC=∠ABC=

1

2

×30°=15°；
③如图3，点A是底角顶点，且AD在△ABC内部时，
∵AD=

1

2

BC，AC=BC，
∴AD=

1

2

AC，
∴∠C=30°，
∴∠BAC=∠ABC=

1

2

（180°-30°）=75°；
综上所述，△ABC底角的度数为45°或15°或75°．
故选C．