题目内容
如图,在△ABC中,AB=AC,∠BAC=30°,分别以AB、AC为边向形外作两个等腰直角三角形ABD和ACE,使∠BAD=∠CAE=90°.
(1)求∠DBC的度数;
(2)求证:BD=CE;
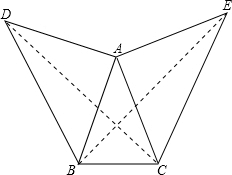
(3)若连接BE、CD,试判断BE、CD是否相等,并对结论给予证明.
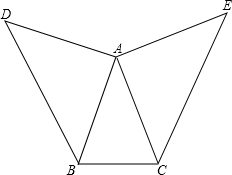
(1)求∠DBC的度数;
(2)求证:BD=CE;
(3)若连接BE、CD,试判断BE、CD是否相等,并对结论给予证明.

(1)∵AB=AC,∠BAC=30°,
∴∠ABC=∠ACB=
=75°,
∵以AB、AC为边向形外作两个等腰直角三角形ABD和ACE,
∴∠ABD=∠ACE=45°,
∴∠DBC=75°+45°=120°;
(2)证明:∵△ADB和△ACE都是等腰直角三角形,且AB=AC,
∴AB=AD=AC=AE,
在△ADB和△ACE中,
,
∴△ADB≌△ACE(SAS),
∴BD=EC;
(3)BE=CD,
理由:由(2)得,AB=AD=AC=AE,∠EAC=∠DAB=90°,
∴∠EAB=∠DAC,
∴在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴BE=CD.
∴∠ABC=∠ACB=
| 180°-30° |
| 2 |
∵以AB、AC为边向形外作两个等腰直角三角形ABD和ACE,
∴∠ABD=∠ACE=45°,
∴∠DBC=75°+45°=120°;
(2)证明:∵△ADB和△ACE都是等腰直角三角形,且AB=AC,
∴AB=AD=AC=AE,
在△ADB和△ACE中,
|
∴△ADB≌△ACE(SAS),
∴BD=EC;
(3)BE=CD,
理由:由(2)得,AB=AD=AC=AE,∠EAC=∠DAB=90°,
∴∠EAB=∠DAC,
∴在△DAC和△BAE中,
|
∴△DAC≌△BAE(SAS),
∴BE=CD.


练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目