题目内容
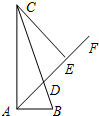
在直角三角形ABC中，∠CAB=90°，∠ABC=72°，AD是∠CAB的角平分线，交边BC于点D，过点C作△ACD中AD边上的高线CE，则∠ECD的度数为（ ）
| A．63° | B．45° | C．27° | D．18° |
∵∠CAB=90°，AD是∠CAB的角平分线，
∴∠CAD=
×90°=45°，
∵CE⊥AD，
∴∠ACE=90°-45°=45°，
又∵∠CAB=90°，∠ABC=72°，
∴∠ACB=90°-72°=18°，
∴∠ECD=∠ACE-∠ACB=45°-18°=27°．
故选C．
∴∠CAD=
| 1 |
| 2 |
∵CE⊥AD，
∴∠ACE=90°-45°=45°，
又∵∠CAB=90°，∠ABC=72°，
∴∠ACB=90°-72°=18°，
∴∠ECD=∠ACE-∠ACB=45°-18°=27°．
故选C．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
