题目内容
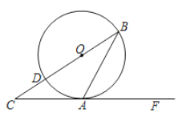
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
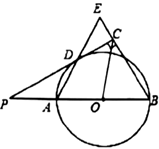
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)连接OD,由PD切 O于点D,得到OD⊥PD,由于BE⊥PC,得到OD∥BE,得出∠ADO=∠E,根据等腰三角形的性质和等量代换可得结论;(Ⅱ)由平行线的性质可得∠DOP=60°,利用三角函数可求出OD、OP、PC的长,即可得CD的长,利用勾股定理求出OC的长即可.
(Ⅰ)连接![]() ,
,
∵PD切![]() 于点
于点![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅱ)∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴OD=2,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴DC=PC-PD=![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目