题目内容
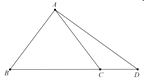
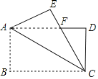
【题目】如图,![]() 为
为![]() 的外接圆,
的外接圆,![]() 为
为![]() 与
与![]() 的交点,
的交点,![]() 为线段
为线段![]() 延长线上一点,且
延长线上一点,且![]() .
.
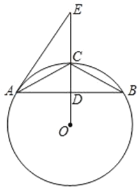
(1)求证:直线![]() 是
是![]() 的切线.
的切线.
(2)若![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②求![]() 的内心到点
的内心到点![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)①![]() ;②5.
;②5.
【解析】
(1)连接AO,并延长AO交⊙O于点F,连接CF,由圆周角定理的推论可得∠ACF=90°,可得∠F+∠FAC=90°,由∠EAC=∠ABC,可得∠EAC+∠FAC=90°,即可完成证明;
(2)①由垂径定理可得OD⊥AB,AD=BD=8,由勾股定理可求⊙O的半径;
②作∠CAB的平分线交CD于点H,连接BH,过点H作HM⊥AC,HN⊥BC,则点H是△ABC的内心,由三角形内心的性质可得HM=HN=HD,由三角形的面积公式可求HD的值,即可完成解答.
(1)证明:如图:连接AO,并延长AO交⊙O于点F,连接CF,
∵AF是直径,
∴∠ACF=90°,
∴∠F+∠FAC=90°,
∵∠F=∠ABC,∠ABC=∠EAC,
∴∠EAC=∠F,
∴∠EAC+∠FAC=90°,
∴∠EAF=90°,
∵AO是半径,
∴直线AE是⊙O的切线;

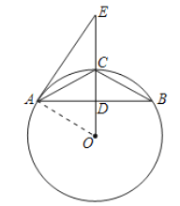
(2)①如图,连接AO,
∵D为AB的中点,OD过圆心,
∴OD⊥AB,AD=BD=![]() AB=8,
AB=8,
∵AO2=AD2+DO2,
∴AO2=82+(AO-6)2,
∴AO=![]() ,
,
∴⊙O的半径为![]() ;
;
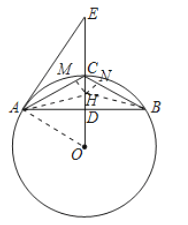
②如图,作∠CAB的平分线交CD于点H,连接BH,过点H作HM⊥AC,HN⊥BC,
∵OD⊥AB,AD=BD,
∴AC=BC,
∴CD平分∠ACB,即点H是△ABC的内心,
∴MH=NH=DH,
在Rt△ACD中,![]() ,
,
∵S△ABC=S△ACH+S△ABH+S△BCH,
∴![]() ×16×6=
×16×6=![]() ×10×MH+
×10×MH+![]() ×16×DH+
×16×DH+![]() ×10×NH,
×10×NH,
∴DH=![]() ,
,
∵OH=CO-CH=CO-( CD-DH),
∴![]() .
.

【题目】学校开设“慈善基金”活动以来,受到同学们的广泛帮助,学校为了解全校学生捐款的情况,随机调查了部分学生的捐款金额,并制成如图不完整的统计图表.
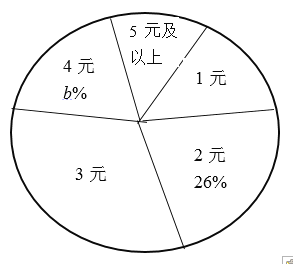
捐款金额 | 1元 | 2元 | 3元 | 4元 | 5元及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)该调查统计数据的中位数是 ,众数是 ;
(3)请计算扇形统计图中的3元所对应的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,统计该校学生在5元及以上的人数.