题目内容
【题目】如图，在平面直角坐标系中，⊙M过原点O，与x轴交于A（4，0），与y轴交于B（0，3），点C为劣弧AO的中点，连接AC并延长到D，使DC=4CA，连接BD． 
（1）求⊙M的半径；
（2）证明：BD为⊙M的切线；
（3）在直线MC上找一点P，使|DP﹣AP|最大．
【答案】
（1）解：∵由题意可得出：OA2+OB2=AB2，AO=4，BO=3，
∴AB=5，
∴圆的半径为 
（2）证明：由题意可得出：M（2， 
）
又∵C为劣弧AO的中点，由垂径定理且 MC= ，故 C（2，﹣1）
过 D 作 DH⊥x 轴于 H，设 MC 与 x 轴交于 K，
则△ACK∽△ADH，
又∵DC=4AC，
故 DH=5KC=5，HA=5KA=10，
∴D（﹣6，﹣5）
设直线AB表达式为：y=kx+b，
，
解得：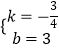 
故直线AB表达式为：y=﹣ 
x+3，
同理可得：根据B，D两点求出BD的表达式为y= 
x+3，
∵kAB×kBD=﹣1，
∴BD⊥AB，BD为⊙M的切线
（3）解：取点A关于直线MC的对称点O，连接DO并延长交直线MC于P，
此P点为所求，且线段DO的长为|DP﹣AP|的最大值；
设直线DO表达式为 y=kx，
∴﹣5=﹣6k，
解得：k= 
，
∴直线DO表达式为 y= x
又∵在直线DO上的点P的横坐标为2，y= 
，
∴P（2， ），
此时|DP﹣AP|=DO= 
= 
【解析】（1）利用A，B点坐标得出AO，BO的长，进而得出AB的长，即可得出圆的半径；（2）根据A，B 两点求出直线AB表达式为：y=﹣ x+3，根据 B，D 两点求出 BD 表达式为 y= x+3，进而得出BD⊥AB，求出BD为⊙M的切线；（3）根据D，O两点求出直线DO表达式为 y= x 又在直线 DO 上的点P的横坐标为2，所以 p（2， ），此时|DP﹣AP|=DO= ．
