题目内容
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).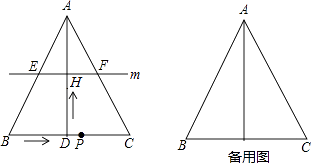
(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.
【答案】
(1)
证明:当t=2时,DH=AH=4,则H为AD的中点,如答图1所示.

又∵EF⊥AD,
∴EF为AD的垂直平分线,
∴AE=DE,AF=DF.
∵AB=AC,AD⊥BC于点D,
∴AD⊥BC,∠B=∠C.
∴EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴∠AEF=∠AFE,
∴AE=AF,
∴AE=AF=DE=DF,即四边形AEDF为菱形.
(2)
解:如答图2所示,
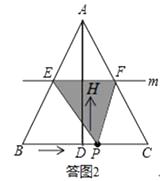
由(1)知EF∥BC,
∴△AEF∽△ABC,
∴ ![]() ,即
,即 ![]() ,解得:EF=10﹣
,解得:EF=10﹣ ![]() t.
t.
S△PEF= ![]() EFDH=
EFDH= ![]() (10﹣
(10﹣ ![]() t)2t=﹣
t)2t=﹣ ![]() t2+10t=﹣
t2+10t=﹣ ![]() (t﹣2)2+10(0<t<
(t﹣2)2+10(0<t< ![]() ),
),
∴当t=2秒时,S△PEF存在最大值,最大值为10cm2,此时BP=3t=6cm
(3)
解:存在.理由如下:
①若点E为直角顶点,如答图3①所示,
此时PE∥AD,PE=DH=2t,BP=3t.
∵PE∥AD,∴ ![]() ,即
,即 ![]() ,此比例式不成立,故此种情形不存在;
,此比例式不成立,故此种情形不存在;
②若点F为直角顶点,如答图3②所示,
此时PF∥AD,PF=DH=2t,BP=3t,CP=10﹣3t.
∵PF∥AD,∴ ![]() ,即
,即 ![]() ,解得t=
,解得t= ![]() ;
;
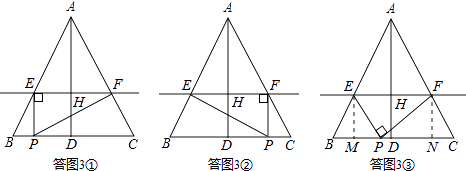
③若点P为直角顶点,如答图3③所示.
过点E作EM⊥BC于点M,过点F作FN⊥BC于点N,则EM=FN=DH=2t,EM∥FN∥AD.
∵EM∥AD,∴ ![]() ,即
,即 ![]() ,解得BM=
,解得BM= ![]() t,
t,
∴PM=BP﹣BM=3t﹣ ![]() t=
t= ![]() t.
t.
在Rt△EMP中,由勾股定理得:PE2=EM2+PM2=(2t)2+( ![]() t)2=
t)2= ![]() t2.
t2.
∵FN∥AD,∴ ![]() ,即
,即 ![]() ,解得CN=
,解得CN= ![]() t,
t,
∴PN=BC﹣BP﹣CN=10﹣3t﹣ ![]() t=10﹣
t=10﹣ ![]() t.
t.
在Rt△FNP中,由勾股定理得:PF2=FN2+PN2=(2t)2+(10﹣ ![]() t)2=
t)2= ![]() t2﹣85t+100.
t2﹣85t+100.
在Rt△PEF中,由勾股定理得:EF2=PE2+PF2,
即:(10﹣ ![]() t)2=(
t)2=( ![]() t2)+(
t2)+( ![]() t2﹣85t+100)
t2﹣85t+100)
化简得: ![]() t2﹣35t=0,
t2﹣35t=0,
解得:t= ![]() 或t=0(舍去)
或t=0(舍去)
∴t= ![]() .
.
综上所述,当t= ![]() 秒或t=
秒或t= ![]() 秒时,△PEF为直角三角形
秒时,△PEF为直角三角形
【解析】(1)如答图1所示,利用菱形的定义证明;(2)如答图2所示,首先求出△PEF的面积的表达式,然后利用二次函数的性质求解;(3)如答图3所示,分三种情形,需要分类讨论,分别求解.

【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果 | 乙种糖果 | 丙种糖果 | |
单价(元/千克) | 15 | 25 | 30 |
千克数 | 40 | 40 | 20 |
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?




