题目内容
【题目】如图，二次函数y=﹣x2+bx+c的图象经过坐标原点，与x轴交于点A（﹣2，0）．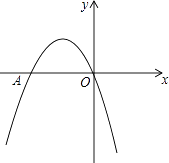 
（1）求此二次函数的解析式；
（2）在抛物线上有一点P，满足S△AOP=1，请直接写出点P的坐标．
【答案】
（1）解：将A（﹣2，0）、O（0，0）代入解析式y=﹣x2+bx+c，得c=0，﹣4﹣2b+c=0，
解得c=0，b=﹣2，
所以二次函数解析式：y=﹣x2﹣2x=﹣（x+1）2+1
（2）解：∵AO=2，S△AOP=1，
∴P点的纵坐标为：±1，
∴﹣x2﹣2x=±1，
当﹣x2﹣2x=1，解得：x1=x2=﹣1，
当﹣x2﹣2x=﹣1时，
解得：x1=﹣1+ 
，x2=﹣1﹣ ，
∴点P的坐标为（﹣1，1）或（﹣1+ ，﹣1））或（﹣1﹣ ，﹣1）
【解析】（1）把A（﹣2，0）、O（0，0）代入解析式y=﹣x2+bx+c，可得出二次函数解析式；（2）利用三角形的面积可得出P点的纵坐标，可求出点P的横坐标，即可得出点P的坐标．
练习册系列答案
相关题目
