题目内容
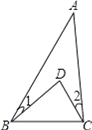
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
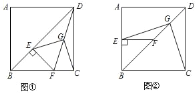
(1)求证:EG=CG;
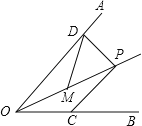
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.
问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用直角三角形斜边上的中线等于斜边长度的一半即可证明;
(2)延长EG、AD交于P点,连接CE、CP,先证明△EGF≌△DGP,再证明△BEC≌△DPC,从而得到△ECP是等腰直角三角形,由△EGF≌△DGP可得G是EP中点,故可证明结论仍然成立.
证明:(1)∵在Rt△DEF中,EG是斜边上的中线
∴DF=2EG
∵在Rt△DCF中,CG是斜边上的中线
∴DF=2CG
∴EG=CG
(2)如图2

延长EG,AD交于P点,连接CE,CP
∵四边形ABCD是正方形
∴BC=CD,AD∥BC,∠ABC=∠ADC=90°,∠ABD=45°
∵EF⊥AB
∴∠ABD=∠EFB=45°
∴EF=BE
∵AD⊥AB,EF⊥AB
∴EF∥AD
∴∠DPE=∠PEF,且DG=GF,∠EGF=DGP
∴△EGF≌△DGP
∴EG=GP,EF=DP
∴BE=DP且BC=CD,∠EBC=∠PDC=90°
∴△BEC≌△DPC
∴EC=PC,∠ECB=∠ECP
∵∠ECB+∠ECD=90°
∴∠DCP+∠ECD=90°
∴∠ECP=90°且EC=CP
∴△ECP是等腰直角三角形,且EG=GP
∴CG⊥EP,CG=EG.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目