题目内容
【题目】如图，已知二次函数y=﹣ 
+bx+c的图象经过A（2，0）、B（0，﹣6）两点．
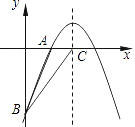
（1）求这个二次函数的解析式；
（2）设该二次函数的对称轴与x轴交于点C，连接BA，BC，求△ABC的面积．
【答案】
（1）
解：把A（2，0）、B（0，﹣6）代入y=﹣ 
+bx+c，
得： 
解得 
，
∴这个二次函数的解析式为y=﹣ +4x﹣6
（2）
解：∵该抛物线对称轴为直线x=﹣ 
=4，
∴点C的坐标为（4，0），
∴AC=OC﹣OA=4﹣2=2，
∴S△ABC= 
×AC×OB= ×2×6=6
【解析】（1）二次函数图象经过A（2，0）、B（0，﹣6）两点，两点代入y=﹣ +bx+c，算出b和c，即可得解析式．（2）先求出对称轴方程，写出C点的坐标，计算出AC，然后由面积公式计算值．
【考点精析】认真审题，首先需要了解二次函数的图象(二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点)．
练习册系列答案
小学教材完全解读系列答案
相关题目
