题目内容
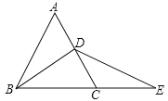
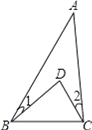
【题目】如图，∠1=20°，∠2=25°，∠A=35°，求∠BDC的度数.
【答案】80°
【解析】
先根据三角形内角和定理得到∠1+∠DBC+∠2+∠DCB+∠A=180°，则可计算出∠DBC+∠DCB=100゜，然后再在△BDC中利用三角形内角和定理计算∠BDC的度数．
解法一、∵在△ABC中，∠1=20°,∠2=25°,∠A=35°,
∴∠DBC+∠DCB=180°﹣20°﹣25°﹣35°=100°,
∴在△BDC中，∠BDC=180°﹣（∠DBC+∠DCB）=180°-100°=80°;
解法二、延长AD，
∵∠3=∠1+∠BAD，∠4=∠2+∠CAD，
∴∠BDC=∠3+∠4
=∠1+∠BAD+∠2+∠CAD
=∠1+∠2+∠BAC
=20°+25°+35°
=80°．
练习册系列答案
相关题目
