题目内容
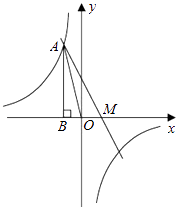
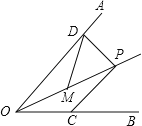
【题目】如图,![]() 是
是![]() 的角平分线上的一点,
的角平分线上的一点,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上的一个动点,若
上的一个动点,若![]() 的最小值为
的最小值为![]() ,则
,则![]() 的长度为____
的长度为____![]() .
.
【答案】![]()
【解析】
如图,过点P作PN⊥OB,垂足为N,根据角平分线的定义可得∠AOP=![]() ∠AOB=30°,再根据直角三角形的性质求得PD=
∠AOB=30°,再根据直角三角形的性质求得PD=![]() OP,然后根据角平分线的性质和垂线段最短得到PD的长,继而根据直角三角形斜边中线等于斜边的一半即可求得结果.
OP,然后根据角平分线的性质和垂线段最短得到PD的长,继而根据直角三角形斜边中线等于斜边的一半即可求得结果.
如图,过点P作PN⊥OB,垂足为N,
∵P是∠AOB角平分线上的一点,∠AOB=60°,
∴∠AOP=![]() ∠AOB=30°,
∠AOB=30°,
又∵PD⊥OA,
∴PD=![]() OP,PN=PD,
OP,PN=PD,
∵点C是OB上一个动点,
∴PC的最小值为P到OB距离,即PN=PC的最小值=3,
∴PD =3,
∴OP=6,
又∵M是OP的中点,
∴DM=![]() OP=3,
OP=3,
故答案为:3.

练习册系列答案
相关题目