题目内容
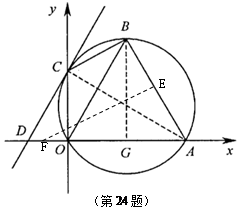
已知:如图,在直角坐标系xoy中,点A(2,0),点B在第一象限且△OAB为正三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.
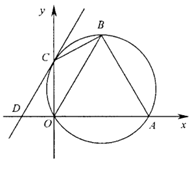
小题1:(1)求B、C两点的坐标;
小题2:(2)求直线CD的函数解析式;
小题3:(3)设E、F分别是线段AB、AD上的两个动点,且EF平分四边形ABCD的周长.
试探究:当点E运动到什么位置时,△AEF的面积最大?最大面积是多少?

小题1:(1)求B、C两点的坐标;
小题2:(2)求直线CD的函数解析式;
小题3:(3)设E、F分别是线段AB、AD上的两个动点,且EF平分四边形ABCD的周长.
试探究:当点E运动到什么位置时,△AEF的面积最大?最大面积是多少?
小题1:解:(1)∵A(2,0),
∴OA=2.
作BG⊥OA于G,
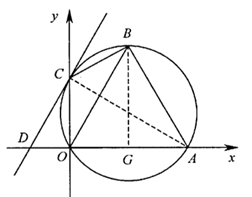
∵△OAB为正三角形,∴OG=1,BG=
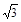 ,
,∴B(1,
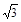 ). ………………………………1分
). ………………………………1分连AC,∵∠AOC=90°,∠ACO=∠ABO=60°.
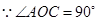 ,∴OC=
,∴OC=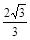 .
. ∴C(0,
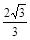 ). …………………………………2分
). …………………………………2分小题2:(2)∵∠AOC=90°,∴AC是圆的直径,
又∵CD是圆的切线,∴CD⊥AC.
∴∠OCD=30°,OD=
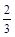 .∴D(
.∴D(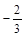 ,0).
,0).设直线CD的函数解析式为y=kx+b(k≠0),
则
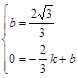 ,解得
,解得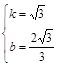
∴直线CD的解析式为y=
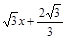 .…4分
.…4分小题3:(3)∵AB=OA=2,OD=
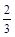 ,CD=2OD=
,CD=2OD=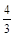 ,BC=OC=
,BC=OC=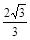 ,
, ∴四边形ABCD的周长6+
∴四边形ABCD的周长6+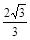 .
.设AE=t,△AEF的面积为S,
则AF=3+
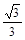 -t,S=
-t,S=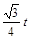 (3+
(3+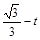 ).
).∵S=
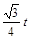 (3+
(3+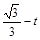 )=
)=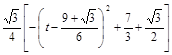 .
.∵点E、F分别在线段AB、AD上,
∴
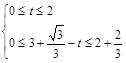 ∴
∴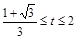 …………………………6分
…………………………6分∴当t=
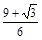 时,S最大=
时,S最大=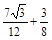 .…………8分
.…………8分略

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 +
+
 于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):(6分)
于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):(6分)
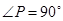 ,
,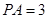 ,那么⊙O的
,那么⊙O的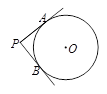
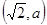 (a>0),半径为
(a>0),半径为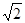 ,函数
,函数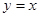 的图象被⊙P截得的弦AB的长为2.
的图象被⊙P截得的弦AB的长为2.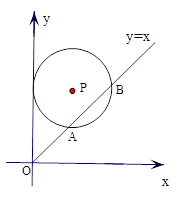
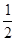 ,求⊙O的直径.
,求⊙O的直径.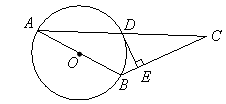
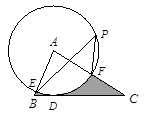

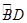 ,则图中阴影部分的面积是_________.
,则图中阴影部分的面积是_________.
 A交圆于E.
A交圆于E.