题目内容
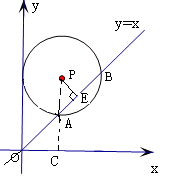
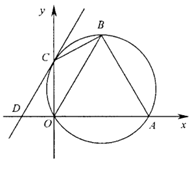
如图,在平面直角坐标系中,⊙P的圆心是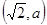 (a>0),半径为
(a>0),半径为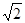 ,函数
,函数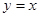 的图象被⊙P截得的弦AB的长为2.
的图象被⊙P截得的弦AB的长为2.
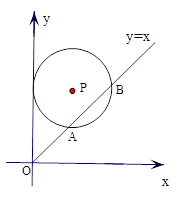
小题1:(1)试判断y轴与圆的位置关系,并说明理由.
小题2:(2)求a的值.
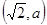 (a>0),半径为
(a>0),半径为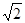 ,函数
,函数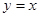 的图象被⊙P截得的弦AB的长为2.
的图象被⊙P截得的弦AB的长为2.
小题1:(1)试判断y轴与圆的位置关系,并说明理由.
小题2:(2)求a的值.
小题1:解:(1)答:y轴与⊙P相切.-------1分
∵点P的坐标为
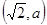 .
.∴点P到y轴的距离为
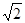 ----------2分
----------2分∵⊙P的半径为
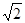
∴点P到y轴的距离=⊙P的半径
∴y轴与⊙P相切.-
小题2:(2)过点P作PE⊥AB于点E,
联结PA并延长PA交x轴于点C. -----4分
∵PE⊥AB,AB=2∴AE=
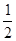 AB="1." --------5分
AB="1." --------5分∵PA=
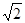
在Rt△PAE中,由勾股定理得:PE=1
∴PE="AE," ∴∠PAE=45°
∵函数
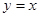 的图象与
的图象与 y轴的夹角为45°
y轴的夹角为45°∴y轴∥PA,∴∠PC
 O=90°
O=90°∴A点的横坐标为
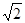
∵A点在直线
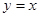 上,∴A点的纵坐标为
上,∴A点的纵坐标为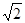
∴PC=

∴a=

略

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

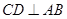 于
于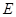 ,若
,若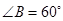 ,则
,则 度.
度.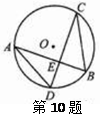
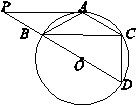
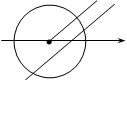
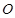 是以数轴的原点
是以数轴的原点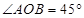 ,点
,点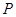 (P与O不重合)在数轴上运动,若过点
(P与O不重合)在数轴上运动,若过点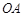 平行的直线与⊙
平行的直线与⊙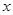 ,则
,则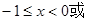
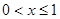
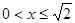
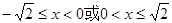
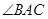 ,
,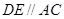 ,且
,且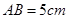 ,求DE的长.
,求DE的长.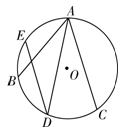
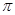 ㎝2
㎝2