题目内容
【题目】在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
(1)旋转过程中,当MN和AC平行时,求正方形OABC旋转的角度;
(2)试证明旋转过程中,△MNO的边MN上的高为定值;
(3)折△MBN的周长为p,在旋转过程中,p值是否发生变化?若发生变化,说明理由;若不发生变化,请给予证明,并求出p的值.
【答案】
(1)
解:如图1中,
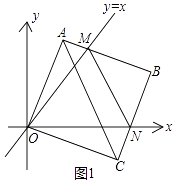
∵四边形OABC是正方形,
∴∠BAC=∠BCA=45°,BA=BC,OA=OC,∠OAB=∠OCB=90°
∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°,
∴∠BMN=∠BNM.
∴BM=BN,
∴AM=CN.
在△OAM与△OCN中,
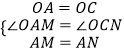
∴△OAM≌△OCN(SAS),
∴∠AOM=∠CON,
∴∠AOM=∠CON=22.50,
∴MN∥AC时,旋转角为22.50.
(2)
解:证明:如图2中,
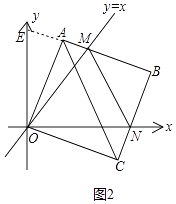
过点O作OF⊥MN于F,延长BA交y轴与E点,则∠AOE=45°﹣∠AOM,∠CON=45°﹣∠AOM.
∴∠AOE=∠CON.
在△OAE与△OCN中,
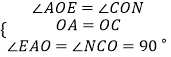
∴△OAE≌△OCN(ASA),
∴OE=ON,AE=CN.
在△OME与△OMN中,
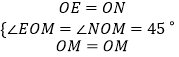
∴△OME≌△OMN(SAS),
∴∠OME=∠OMN.
∵MA⊥OA,MF⊥OF.
∴OA=OF=2,
∴在旋转过程中,高为定值.
(3)
解:旋转过程中,p值不变化.
理由:∵△OME≌△OMN,
∴ME=MN,
∵AE=CN,
∴MN=ME﹣AM+AE=AM+CN.
∴p=MN+BN+BM=AM+CN+BN+BM=AB+AC=4.
∴△MBN的周长p为定值.
【解析】(1)只要证明△AOM≌△CON,推出∠AOM=∠CON=22.5°即可解决问题.(2)如图2中,过点O作OF⊥MN于F,延长BA交y轴与E点,则∠AOE=45°﹣∠AOM,∠CON=45°﹣∠AOM.先证明△OAE≌△OCN(ASA),再证明△OME≌△OMN(SAS),推出∠OME=∠OMN,利用角平分线性质定理即可解决问题.(3)由(2)可知,MN=AM+CN,可以推出△BMN的周长为BA+BC是定值.
【考点精析】本题主要考查了图形的旋转的相关知识点,需要掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能正确解答此题.