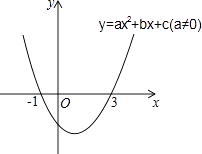题目内容
【题目】如图,在△ABC中,BC边上的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC于点G.
求证:(1)BF=CG;
(2)AB+AC=2AF.
【答案】(1) 见解析;(2)见解析
【解析】
(1)连接EB、EC,利用已知条件证明Rt△BEF≌Rt△CEG,即可得到BF=CG;
(2)根据(1)中的条件证得Rt△AFE≌Rt△AGE,根据全等三角形的性质得到AG=AF,于是得到结论.
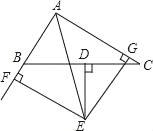
(1)如图,连接BE和CE.
∵DE是BC的垂直平分线,
∴BE=CE.
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴∠BFE=∠EGC=90°,EF=EG.
在Rt△BFE和Rt△CGE中,
BE=CE,EF=EG,
∴Rt△BFE≌Rt△CGE(HL),
∴BF=CG.
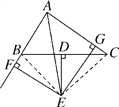
(2)∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴∠AFE=∠AGE=90°,∠FAE=∠GAE.
在△AFE和△AGE中,
∠FAE=∠GAE ,∠AFE=∠AGE,AE=AE,
∴△AFE≌△AGE,∴AF=AG.
∵BF=CG,
∴AB+AC=AF-BF+AG+CG=2AF.

练习册系列答案
相关题目