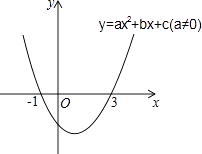题目内容
【题目】如图，直线L：y=-
x+2与x轴、y轴分别交于A、B两点，在y轴上有一点C（0，4），动点M从A点以每秒1个单位的速度沿x轴向左移动．
（1）求A、B两点的坐标；
（2）求△COM的面积S与M的移动时间t之间的函数关系式；
（3）当t为何值时△COM≌△AOB，并求此时M点的坐标．
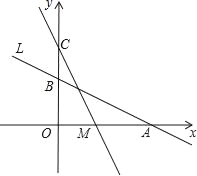
【答案】（1）A（4，0）、B（0，2）；（2）当0≤t≤4时， S△OCM=8﹣2t；当t＞4时，S△OCM=2t﹣8；（3）（2，0）或（﹣2，0）
【解析】试题分析：解：
（1）
与x轴、y轴分别交于A、B两点
所以y=0时，x=4，故A（4,0）
交y轴于B，则有：x=0，y=2
所以B(0,2)
（2）则有OM=
，OC=4
所以S=2
（3）△COM≌△AOB，则有两种情况，完全重合时，则有M(2,0)
对称时：M（-2，0）
练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列说法正确的是（ ）
A.抛物线的开口向下
B.当x＞﹣3时，y随x的增大而增大
C.二次函数的最小值是﹣2
D.抛物线的对称轴是x=﹣ 
