题目内容
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连接DF,则下列四个结论中,错误的是( )
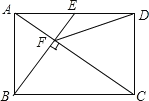
A. △AEF~△CABB. CF=2AFC. DF=DCD. tan∠CAD=![]()
【答案】D
【解析】
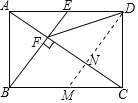
根据四边形ABCD是矩形,BE⊥AC,可得∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB,故A正确;根据点E是AD边的中点,以及AD∥BC,得出△AEF∽△CBF,根据相似三角形对应边成比例,可得CF=2AF,故B正确;过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=![]() BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故C正确;设AE=a,AB=CD=b,则AD=2a,通过证明△BAE∽△ADC,可得
BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故C正确;设AE=a,AB=CD=b,则AD=2a,通过证明△BAE∽△ADC,可得![]() =
=![]() ,进而可得b=
,进而可得b=![]() a,根据正切的定义可得tan∠CAD=
a,根据正切的定义可得tan∠CAD=![]() =
=![]() =
=![]() ,即可证明D错误.
,即可证明D错误.
如图,过D作DM∥BE交AC于N,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故A正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴![]() =
=![]() ,
,
∵AE=![]() AD=
AD=![]() BC,
BC,
∴![]() =
=![]() ,
,
∴CF=2AF,故B正确;
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=![]() BC,
BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DM垂直平分CF,
∴DF=DC,故C正确;
设AE=a,AB=CD=b,则AD=2a,
∵∠ABE+∠AEB=90°,∠FAE+∠AEB=90°,
∴∠BAE=∠FAE,
∵∠AFE=∠ADC=90°,
∴△BAE∽△ADC,
∴![]() ,即
,即![]() =
=![]() ,
,
∴b=![]() a,
a,
∴tan∠CAD=![]() =
=![]() =
=![]() ,故D错误;
,故D错误;
故选D.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案