题目内容
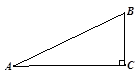
丽水市在规划新城期间,欲拆除瓯江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)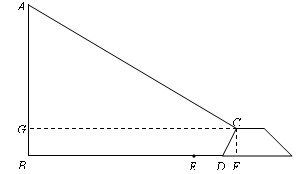

解:由tan∠CDF=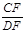 =2,CF=2米
=2,CF=2米
∴DF=1米,BG=2米
∵BD=14米
∴BF=GC=15米
在Rt△AGC中,由tan30°=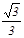
∴AG=15×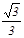 =
=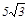
≈5×1.732=8.660米
∴AB=8.660+2=10.66米
BE=BD-ED=12米
∵BE>AB
∴不需要封人行道
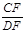 =2,CF=2米
=2,CF=2米∴DF=1米,BG=2米
∵BD=14米
∴BF=GC=15米
在Rt△AGC中,由tan30°=
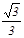
∴AG=15×
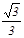 =
=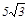
≈5×1.732=8.660米
∴AB=8.660+2=10.66米
BE=BD-ED=12米
∵BE>AB
∴不需要封人行道
构造直角三角形解直角三角形即可。

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
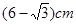
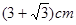
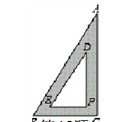
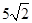 米(BC所在地面为水平面)。(1)改善后的台阶坡面会AD长多少米?(2)改善后的台阶会多占多长一段水平地面?(结果保留根号)
米(BC所在地面为水平面)。(1)改善后的台阶坡面会AD长多少米?(2)改善后的台阶会多占多长一段水平地面?(结果保留根号)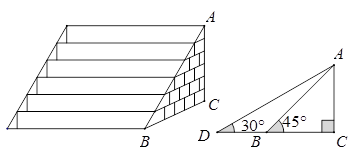
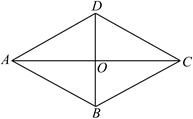
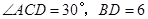 .
. 

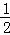
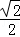
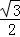
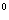 ,sin60
,sin60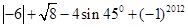 .
.