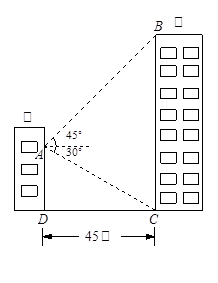题目内容
已知:如图,四边形ABCD是菱形,对角线AC与BD相交于O,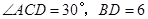 .
.
(1)求证:△ABD是等边三角形;
(2)求 AC的长(结果可保留根号).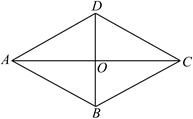
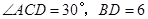 .
. (1)求证:△ABD是等边三角形;
(2)求 AC的长(结果可保留根号).

(1)证明:∵四边形ABCD是菱形
∴∠BCD=2∠ACD.
又∵∠ACD=30°,∴∠BCD=60°.
∵四边形ABCD是菱形
∴∠BAD=∠BCD=60°.
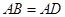 .
.
∴△ABD是等边三角形.
(2)解:∵四边形ABCD是菱形
∴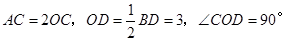
在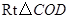 中,
中,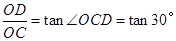 ,
,
∴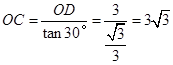
∴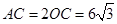 .答
.答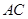 的长为
的长为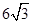 .
.
∴∠BCD=2∠ACD.
又∵∠ACD=30°,∴∠BCD=60°.
∵四边形ABCD是菱形
∴∠BAD=∠BCD=60°.
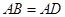 .
. ∴△ABD是等边三角形.
(2)解:∵四边形ABCD是菱形
∴
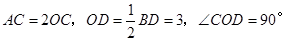
在
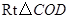 中,
中,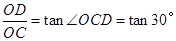 ,
,∴
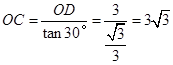
∴
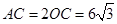 .答
.答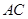 的长为
的长为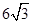 .
. (1)菱形的边AB=AD,即已知两边相等,再寻找一个角为60°,即可证明△ABD是正三角形;
(2)先求OC的长,再求AC.
(2)先求OC的长,再求AC.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
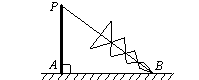
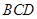 中,∠
中,∠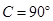 ,∠
,∠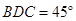 ,利用此等腰直角三角形你能求出
,利用此等腰直角三角形你能求出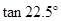 的值吗?
的值吗?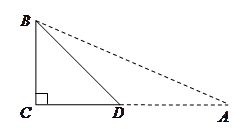
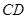 到点
到点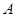 ,使
,使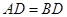 ,连结
,连结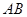 .
.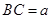 (
(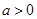 ).
). .
.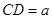 ,
,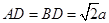 .
.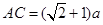 .
.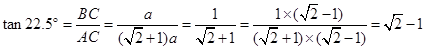 .
.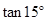 的值;
的值;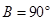 ,∠
,∠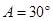 ,
,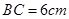 ;图2中,∠
;图2中,∠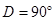 ,∠
,∠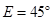 ,
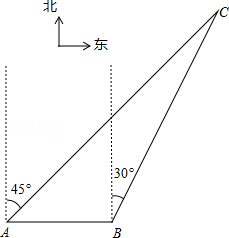
,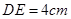 .图3是小刘所做的一个实验:他将△
.图3是小刘所做的一个实验:他将△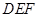 的直角边
的直角边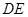 与△
与△ 的斜边
的斜边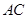 重合在一起,并将△
重合在一起,并将△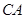 方向移动.在移动过程中,
方向移动.在移动过程中,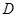 、
、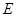 两点始终在
两点始终在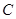 重合).
重合).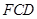 的度数逐渐__________.(填“不变”、“变大”、“变小”)
的度数逐渐__________.(填“不变”、“变大”、“变小”)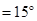 ?如果存在,求出
?如果存在,求出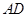 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.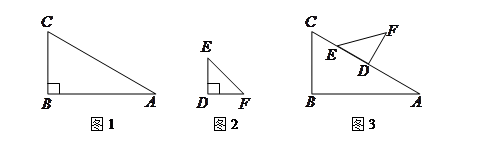
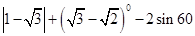 °+
°+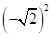
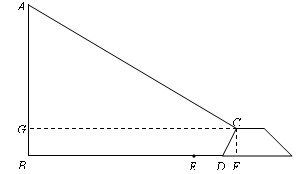
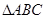 中,
中,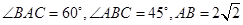 ,
,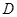 是线段
是线段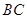 上的一个动点,以
上的一个动点,以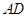 为直径画
为直径画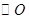 分别交
分别交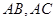 于
于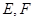 连接
连接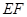 ,则线段
,则线段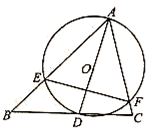
 ,结果精确到1米) .
,结果精确到1米) .