Question

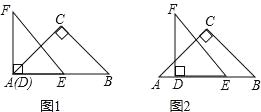
【题目】如图，在矩形ABCD中，E是AD边上的中点，BE⊥AC于F，连接DF，下列4个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④tan∠CAD＝，其中结论正确的序号是______．

Answer 1

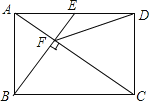
【答案】①②③④

【解析】

①正确．只要证明∠EAC＝∠ACB，∠ABC＝∠AFE＝90°即可；

②正确．由AD∥BC，推出△AEF∽△CBF，推出＝，由AE＝AD＝BC，推出＝，即CF＝2AF；

③正确．只要证明DM垂直平分CF，即可证明；

④正确．设AE＝a，AB＝b，则AD＝2a，由△BAE∽△ADC，有＝，即b＝a，可得tan∠CAD＝＝＝．

如图，过D作DM∥BE交AC于N，

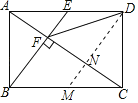
∵四边形ABCD是矩形，

∴AD∥BC，∠ABC＝90°，AD＝BC，

∵BE⊥AC于点F，

∴∠EAC＝∠ACB，∠ABC＝∠AFE＝90°，

∴△AEF∽△CAB，故①正确；

∵AD∥BC，

∴△AEF∽△CBF，

∴＝，

∵AE＝AD＝BC，

∴＝，

∴CF＝2AF，故②正确；

∵DE∥BM，BE∥DM，

∴四边形BMDE是平行四边形，

∴BM＝DE＝BC，

∴BM＝CM，

∴CN＝NF，

∵BE⊥AC于点F，DM∥BE，

∴DN⊥CF，

∴DM垂直平分CF，

∴DF＝DC，故③正确；

设AE＝a，AB＝b，则AD＝2a，

由△BAE∽△ADC，有＝，即b＝a，

∴tan∠CAD＝＝＝．故④正确；

故答案为①②③④．