题目内容
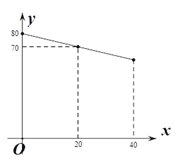
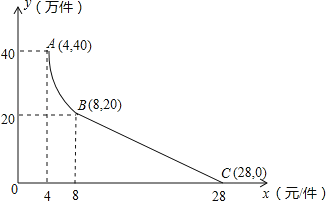
【题目】某公司用100万元研发一种市场急需电子产品,已于当年投入生产并销售,已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,设公司销售这种电子产品的年利润为s(万元).
(1)请求出y(万件)与x(元/件)的函数表达式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)的函数表达式,并求出第一年年利润的最大值.
【答案】(1)y=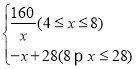 ;(2)当每件的销售价格定为16元时,第一年年利润的最大值为44万元.
;(2)当每件的销售价格定为16元时,第一年年利润的最大值为44万元.
【解析】
(1)依据待定系数法,即可求出y(万件)与x(元/件)之间的函数关系式;
(2)分两种情况进行讨论,当x=8时,smax=﹣20;当x=16时,smax=44;根据44>﹣20,可得当每件的销售价格定为16元时,第一年年利润的最大值为44万元.
解:(1)当4≤x≤8时,设y=![]() ,将A(4,40)代入得k=4×40=160,
,将A(4,40)代入得k=4×40=160,
∴y与x之间的函数关系式为y=![]() ;
;
当8<x≤28时,设y=k'x+b,将B(8,20),C(28,0)代入得,
![]() ,
,
解得![]() ,
,
∴y与x之间的函数关系式为y=﹣x+28,
综上所述,y=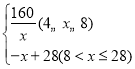 ;
;
(2)当4≤x≤8时,s=(x﹣4)y﹣160=(x﹣4)![]() ﹣100=
﹣100=![]() +60,
+60,
∵当4≤x≤8时,s随着x的增大而增大,
∴当x=8时,smax=![]() +60=﹣20;
+60=﹣20;
当8<x≤28时,s=(x﹣4)y﹣80=(x﹣4)(﹣x+28)﹣80=﹣(x﹣100)2+44,
∴当x=16时,smax=44;
∵44>﹣20,
∴当每件的销售价格定为16元时,第一年年利润的最大值为44万元.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目