题目内容

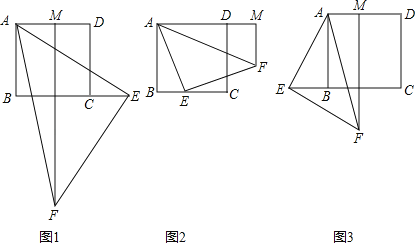
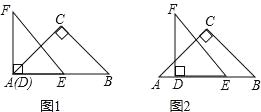
【题目】如图1，△ABC和△DEF都是等腰直角三角形，其中∠C=∠EDF=90°，点A与点D重合，点E在AB上，AB=4，DE=2．如图2，△ABC保持不动，△DEF沿着线段AB从点A向点B移动，当点D与点B重合时停止移动．设AD=x，△DEF与△ABC重叠部分的面积为y，则y关于x的函数图象大致是（ ）

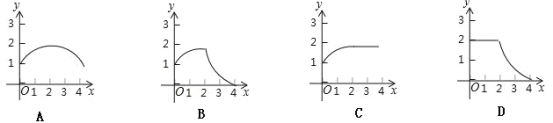
【答案】B.

【解析】

试题解析：由题意知：在△DEF移动的过程中，阴影部分总为等腰直角三角形．

当0＜x≤2时，此时重合部分的斜边长为x，则y=×(x+2）×（x+2）-x2=-x2+x+1．

当2＜x≤4时，此时重合部分的斜边长为2，则y=（x-4）2；

当4＜x≤6时，此时重合部分的斜边长为2-（x-4）=6-x，则y=（6-x）××=x2-3x+9；

由以上分析可知，这个分段函数的图象左边为抛物线的一部分，中间为直线的一部分，右边为抛物线的一部分．

故选B．

练习册系列答案
相关题目

【题目】如图，在平面直角坐标系中，直线与双曲线交于点A，过点作AO的平行线交双曲线于点B，连接AB并延长与y轴交于点，则k的值为______．

【题目】在平面直角坐标系xOy中，抛物线y=ax2-2ax-3a（a≠0）顶点为P，且该抛物线与x轴交于A，B两点（点A在点B的左侧）．我们规定：抛物线与x轴围成的封闭区域称为“G区域”（不包含边界）；横、纵坐标都是整数的点称为整点．

（1）求抛物线y=ax2-2ax-3a顶点P的坐标（用含a的代数式表示）；

（2）如果抛物线y=ax2-3ax-3a经过（1，3）．

①求a的值；

②在①的条件下，直接写出“G区域”内整点的个数．

（3）如果抛物线y=ax2-2ax-3a在“G区域”内有4个整点，直接写出a的取值范围．

【题目】如图，在矩形ABCD中，E是AD边上的中点，BE⊥AC于F，连接DF，下列4个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④tan∠CAD＝，其中结论正确的序号是______．

【题目】已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在BC上，(不与B、C重合)，FM⊥AD，交射线AD于点M．

(1)如图1，当点E在边BC的延长线上，点M在边AD上时，请直接写出线段AB，BE，AM之间的数量关系，不需要证明.

(2)如图2，当点E在边BC上，点M在边AD的延长线上时，请写出线段AB，BE，AM之间的数量关系，并且证明你的结论.

(3)如图3，当点E在边CB的延长线上，点M在边AD上时，若BE＝，∠AFM＝15°，求AM的长度.

【题目】如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE．

（1）求证：四边形ABCD是菱形；

（2）若AB＝，BD＝2，求OE的长．

【题目】如图，在平面直角坐标系中，二次函数的图象交x轴于点A，B（点A在点B的左侧）．

（1）求点A，B的坐标，并根据该函数图象写出y≥0时x的取值范围；

（2）把点B向上平移m个单位得点B1．若点B1向左平移n个单位，将与该二次函数图象上的点B2重合；若点B1向左平移(n＋6)个单位，将与该二次函数图象上的点B3重合．已知m＞0，n＞0，求m，n的值．

【题目】“2019大洋湾盐城马拉松”的赛事共有三项：A，“全程马拉松”、B，“半程马拉松”、C．“迷你健身跑”，小明和小刚参与了该项赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组．

（1）小明被分配到“迷你健身跑”项目组的概率为　 　；

（2）求小明和小刚被分配到不同项目组的概率．

【题目】如图是小强洗漱时的侧面示意图，洗漱台(矩形ABCD)靠墙摆放，高AD=80cm，宽AB=48cm，小强身高166cm，下半身FG=100cm.洗漱时下半身与地面成80°角(即∠FGK=80°)，身体前倾成125°角(即∠EFG=125°)，脚与洗漱台的距离GC=15cm(点D、C、G、K在同一直线上).

(1)求此时小强头部E点与地面DK的距离；

(2)小强希望他的头部E点恰好在洗漱盆AB的中点O的正上方，他应向前或后退多少(结果精确到0.1cm，参考数据：cos80°≈0.17，sin80°≈0.98，≈1.41)？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网