Question

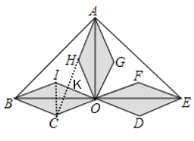
【题目】三个形状大小相同的菱形按如图所示方式摆放，已知∠AOB＝∠AOE＝90°，菱形的较短对角线长为2cm．若点C落在AH的延长线上，则△ABE的周长为________cm．

Answer 1

【答案】

【解析】

连接IC，连接CH交OI于K，则A，H，C在同一直线上，CI＝2，根据△COH是等腰直角三角形，即可得到∠CKO＝90°，即CK⊥IO，设CK＝OK＝x，则CO＝IO＝x，IK＝xx，根据勾股定理即可得出x2＝2＋，再根据S菱形BCOI＝IO×CK＝IC×BO，即可得出BO＝2＋2，进而得到△ABE的周长．

解：如图所示，连接IC，连接CH交OI于K，则A，H，C在同一直线上，CI＝2，

∵三个菱形全等，

∴CO＝HO，∠AOH＝∠BOC，

又∵∠AOB＝∠AOH＋∠BOH＝90°，

∴∠COH＝∠BOC＋∠BOH＝90°，

即△COH是等腰直角三角形，

∴∠HCO＝∠CHO＝45°＝∠HOG＝∠COK，

∴∠CKO＝90°，即CK⊥IO，

设CK＝OK＝x，则CO＝IO＝x，IK＝xx，

∵Rt△CIK中，（xx）2＋x2＝22，

解得x2＝2＋，

又∵S菱形BCOI＝IO×CK＝IC×BO，

∴x2＝×2×BO，

∴BO＝2＋2，

∴BE＝2BO＝4＋4，AB＝AE＝BO＝4＋2，

∴△ABE的周长＝4＋4＋2（4＋2）＝12＋8，

故答案为：12＋8．