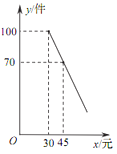
题目内容
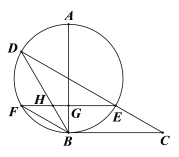
【题目】如图,线段BC所在的直线 是以AB为直径的圆的切线,点D为圆上一点,满足BD=BC,且点C、D位于直径AB的两侧,连接CD交圆于点E. 点F是BD上一点,连接EF,分别交AB、BD于点G、H,且EF=BD.
(1)求证:EF∥BC;
(2)若EH=4,HF=2,求![]() 的长.
的长.
【答案】(1)见解析;(2) ![]()
![]()
【解析】
(1)根据EF=BD可得![]() =
=![]() ,进而得到
,进而得到![]() ,根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”即可得出角相等进而可证.
,根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”即可得出角相等进而可证.
(2)连接DF,根据切线的性质及垂径定理求出GF、GE的长,根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”及平行线求出相等的角,利用锐角三角函数求出∠BHG,进而求出∠BDE的度数,确定![]() 所对的圆心角的度数,根据∠DFH=90°确定DE为直径,代入弧长公式即可求解.
所对的圆心角的度数,根据∠DFH=90°确定DE为直径,代入弧长公式即可求解.
(1)∵EF=BD,
∴![]() =
=![]()
∴![]()
∴∠D=∠DEF
又BD=BC,
∴∠D=∠C,
∴∠DEF=∠C
EF∥BC
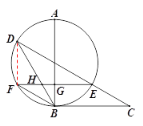
(2)∵AB是直径,BC为切线,
∴AB⊥BC
又EF∥BC,
∴AB⊥EF,弧BF=弧BE,
GF=GE=![]() (HF+EH)=3,HG=1
(HF+EH)=3,HG=1
DB平分∠EDF,
又BF∥CD,
∴∠FBD=∠FDB=∠BDE=∠BFH
∴HB=HF=2
∴cos∠BHG=![]() =
=![]() ,∠BHG=60°.
,∠BHG=60°.
∴∠FDB=∠BDE=30°
∴∠DFH=90°,DE为直径,DE=4![]() ,且弧BE所对圆心角=60°.
,且弧BE所对圆心角=60°.
∴弧BE=![]() ×4
×4![]() =
=![]()
![]()

练习册系列答案
相关题目