题目内容
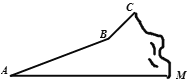
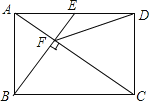
【题目】如图是在写字台上放置一本数学书和一个折叠式台灯时的截面示意图,已知数学书AB长25cm,台灯上半节DE长40cm,下半节CD长50cm.当台灯灯泡E恰好在数学书AB的中点O的正上方时,台灯上、下半节的夹角即∠EDC=105°,下半节CD与写字台FG的夹角即∠DCG=75°,求BC的长.(书的厚度和台灯底座的宽度、高度都忽略不计,F,A,O,B,C,G在同一条直线上,参考数据:sin75°≈0.97,cos75°≈0.26;![]() ≈1.41,
≈1.41,![]() ≈1.73,结果精确到0.1)
≈1.73,结果精确到0.1)

【答案】BC的长约为9.1cm.
【解析】
过点D作DM⊥FG于M,DN⊥EO于N,则四边形DMON是矩形,解直角三角形求出CM和DN的长度,结合矩形的知识求出OM的长,最后根据BC=OM﹣CM﹣BO求出答案.
如图,过点D作DM⊥FG于M,DN⊥EO于N,
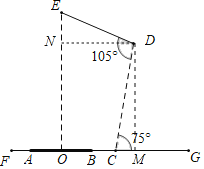
在Rt△CDM中,
∵CD=50,∠DCM=75°,
∴![]() =cos∠DCM,
=cos∠DCM,
∴![]() =cos70°≈0.26,
=cos70°≈0.26,
解得,CM≈13.
∵DN∥FG,
∴∠CDN=∠DCG=75°,
在Rt△DEN中,
∵∠EDN=∠CDE﹣∠CDN=105°﹣75°=30°,DE=40,
∴![]() =cos∠EDN,
=cos∠EDN,
∴![]() =cos30°=
=cos30°=![]() ,
,
解得,DN=20![]() ≈34.6.
≈34.6.
∵∠DNO=∠NOM=∠DMO=90°,
∴四边形DNOM是矩形,
∴OM=DN≈34.6,
∴BC=OM﹣CM﹣BO≈34.6﹣13﹣12.5=9.1(cm).
答:BC的长约为9.1cm.

 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
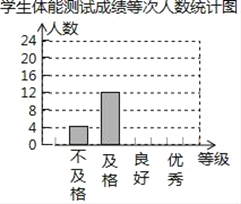
高效智能课时作业系列答案【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级,统计员在将测试数据绘制成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如图图表,请按正确数据解答下列各题:
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 | 8 |
|
良好 | 16 |
|
及格 | 12 |
|
不及格 | 4 |
|
合计 | 40 |
|
(1)填写统计表;
(2)根据调整后数据,补全条形统计图;
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.