Question

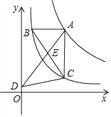
【题目】如图，点A是反比例函数y=图象上的任意一点，过点A作AB∥x轴，AC∥y轴，分别交反比例函数y=的图象于点B，C，连接BC，E是BC上一点，连接并延长AE交y轴于点D，连接CD，则S△DEC﹣S△BEA=_________．

Answer 1

【答案】

【解析】分析：设A（a，），可得B（），C（a，），进而得到AB=a，AC=，依据S△DEC﹣S△BEA=S△DAC﹣S△BCA进行计算即可．

详解：点A是反比例函数y=图象上的任意一点，可设A（a，）．

∵AB∥x轴，AC∥y轴，点B，C，在反比例函数y=的图象上，∴B（），C（a，），∴AB=a，AC=，∴S△DEC﹣S△BEA=S△DAC﹣S△BCA=××（a﹣a）=××a=．

故答案为：．