题目内容
【题目】已知在平面直角坐标系中,A(a,0),B(0,b),D(0,c),其中a,b,c满足2a2+b2+c2-2ab-8a-2c+17=0,过坐标O作直线BC交线段OA于点C.
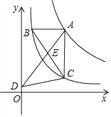
(1)如图1,当∠ODA=∠OCB时,求点C的坐标;

(2)如图2,在(1)条件下,过O作OE⊥BC交AB于点E,过E作EF⊥AD交OA于点N,交BC延长线于F,求证:BF=OE+EF;

【答案】(1)C(1,0);(2)见解析;
【解析】
(1)利用非负数的性质求出a,b,c的值,再证明△AOD≌△BOC(ASA),推出OC=OD=1解决问题;
(2)如图2中,设AD交BC于点Q,连接OQ,QE.想办法证明BQ=OE,FQ=EF即可解决问题;
(1)如图1中,
∵2a2+b2+c2-2ab-8a-2c+17=0,
∴(a-4)2+(a-b)2+(c-1)2=0,
∵(a-4)2≥0,(a-b)2≥0,(c-1)2≥0,
∴a=b=4,c=1,
∴A(4,0),B(0,4),D(0,1).
∴OB=OA,
∵∠ODA=∠OCB,∠AOD=∠BOC=90°,
∴△AOD≌△BOC(ASA),
∴OC=OD=1,
∴C(1,0).
(2)如图2中,设AD交BC于点Q,连接OQ,QE.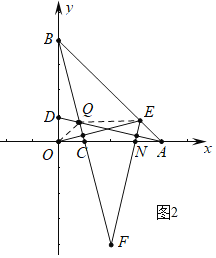
∵△AOD≌△BOC,
∴∠DAO=∠CBO,OD=OC,
∵OB=OA,
∴BD=AC,
∵∠AQB=∠CQA,
∴△DQB≌△CQA(AAS),
∴BQ=AQ,
∵OQ=OQ,OB=OA,BQ=AQ,
∴△OQB≌△OQA(SSS),
∴∠BOQ=∠AOQ=45°,
∴∠BOQ=∠OAE,
∵BF⊥OE,
∴∠OBC+∠BOE=90°,∠BOE+∠AOE=90°,
∴∠OBQ=∠AOE,∵OB=OA,
∴△OBQ≌△AOE(ASA),
∴BQ=OE,OQ=AE,
∵EQ=EQ,AQ=OE,OQ=AE,
∴△OEQ≌△AQE(SSS),
∴∠OEQ=∠AQE,
∵EF⊥AD,OE⊥BC,
∴∠F+∠FEO=90°,∠F+∠FQA=90°,
∴∠FEO=∠FQA,
∴∠FEQ=∠FQE,
∴EF=FQ,
∴BF=BQ+FQ=OE+EF.