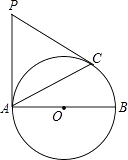题目内容
【题目】如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.

【答案】(1)证明见解析 (2)证明见解析
【解析】
试题(1)根据BF⊥AC,DE⊥AC,AE=CF AF=AE+EF CE=CF+EF,可以证明Rt△ABF≌Rt△CDE,得DE=
BF;再根据BF⊥AC,DE⊥AC,可以证明DE//BF.(2)根据(1)中的结论,可证△BFM≌△DEM,从而证明MB=MD.
试题解析:(1)①DE与BF的关系可以有DE=BF成立,理由如下:
∵AE=CF AF=AE+EF CE=CF+EF
∴AF=CE 又∵BF⊥AC,DE⊥AC
∴∠BFA=∠DEC=90°
在Rt△ABF和Rt△CDE中
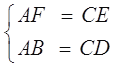
∴Rt△ABF≌Rt△CDE (HL)
∴DE=BF(全等三角形对应边相等)
②DE与BF的关系可以有DE//BF,理由如下:
∵DE⊥AC BF⊥AC
∴DE//BF
(2)证明:
∵Rt△ABF≌Rt△CDE
∴BF=ED
在△BFM和△DEM中
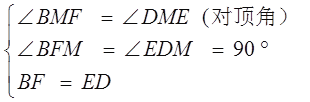
∴△BFM≌△DEM (AAS)
∴MB=MD

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】“十一”期间,包河区牛角大圩60亩的秋季花海是游客观赏的首选景点,有着独具一格的农业风情,花海由矮牵牛、孔雀菊、蓝花鼠尾草、一串红等组成。为了种植“花海”,需要从甲乙两地向大圩A.B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A.B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需人民币).
运费(元/吨) | ||
A | B | |
甲地 | 12 | 12 |
乙地 | 10 | 8 |
(1)设甲地运往![]() 棚营养土
棚营养土![]() 吨,请用关于
吨,请用关于![]() 的代数式完成下表;
的代数式完成下表;
运往A.B两地的吨数 | ||
A | B | |
甲地 |
|
|
乙地 | ___ | ___ |
(2)设甲地运往A棚营养土![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式(要求写出自变量取值范围).
(吨)的函数关系式(要求写出自变量取值范围).
(3)当甲、乙两地各运往A.B两棚多少吨营养土时,总运费最省?最省的总运费是多少?