ƒøƒ⁄»ð
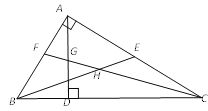
°æƒø°ø»ÁÕº1£¨∂˛¥Œ∫Ø ˝y£Ωax2©Å2ax©Å3a£®a£º0£©µƒÕºœÛ”Îx÷·Ωª”⁄A°¢B¡Ωµ„£®µ„A‘⁄µ„Bµƒ”“≤ý£©£¨”Îy÷·µƒ’˝∞Î÷·Ωª”⁄µ„C£¨∂•µ„Œ™D£Æ
£®1£©«Û∂•µ„Dµƒ◊¯±Í£®”√∫¨aµƒ¥˙ ˝ Ω±Ì æ£©£ª
£®2£©»Ù“‘ADŒ™÷±æ∂µƒ‘≤æ≠π˝µ„C£Æ
¢Ÿ«Û≈◊ŒÔœþµƒ∫Ø ˝πÿœµ Ω£ª
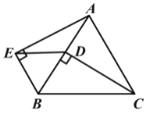
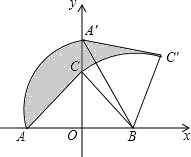
¢⁄»ÁÕº2£¨µ„E «y÷·∏∫∞Î÷·…œ“ªµ„£¨¡¨Ω”BE£¨Ω´°˜OBE»∆∆Ω√ʃ⁄ƒ≥“ªµ„–˝◊™180°„£¨µ√µΩ°˜PMN£®µ„P°¢M°¢N∑÷±∫Õµ„O°¢B°¢E∂‘”¶£©£¨≤¢«“µ„M°¢N∂º‘⁄≈◊ŒÔœþ…œ£¨◊˜MF°Õx÷·”⁄µ„F£¨»Ùœþ∂ŒMF£∫BF£Ω1£∫2£¨«Ûµ„M°¢Nµƒ◊¯±Í£ª
¢€µ„Q‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ£¨“‘QŒ™‘≤–ƒµƒ‘≤π˝A°¢B¡Ωµ„£¨≤¢«“∫Õ÷±œþCDœý«–£¨»ÁÕº3£¨«Ûµ„Qµƒ◊¯±Í£Æ

°æ¥∞∏°ø£®1£©£®1£¨©Å4a£©£ª£®2£©¢Ÿy=©Åx2+2x+3£ª¢⁄M£®![]() £¨
£¨![]() £©°¢N£®
£©°¢N£®![]() £¨
£¨![]() £©£ª¢€µ„Qµƒ◊¯±ÍŒ™£®1£¨©Å4+2
£©£ª¢€µ„Qµƒ◊¯±ÍŒ™£®1£¨©Å4+2![]() £©ªÚ£®1£¨©Å4©Å2
£©ªÚ£®1£¨©Å4©Å2![]() £©£Æ
£©£Æ
°æΩ‚Œˆ°ø
∑÷Œˆ: £®1£©Ω´∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ ΩΩ¯––≈‰∑Ωº¥ø…µ√µΩ∂•µ„Dµƒ◊¯±Í£Æ
£®2£©¢Ÿ“‘ADŒ™÷±æ∂µƒ‘≤æ≠π˝µ„C£¨º¥µ„C‘⁄“‘ADŒ™÷±æ∂µƒ‘≤µƒ‘≤÷Ð…œ£¨“¿æð‘≤÷ÐΩ«∂®¿Ì≤ªƒ—µ√≥ˆ°˜ACD «∏ˆ÷±Ω«»˝Ω«–Œ£¨«“°œACD£Ω90°„£¨Aµ„◊¯±Íø…µ√£¨∂¯C°¢Dµƒ◊¯±Íø…”…a±Ì¥Ô≥ˆ¿¥£¨‘⁄µ√≥ˆAC°¢CD°¢ADµƒ≥§∂»±Ì¥Ô Ω∫Û£¨“¿æðπ¥π…∂®¿Ì¡–µ» Ωº¥ø…«Û≥ˆaµƒ÷µ£Æ
¢⁄Ω´°˜OBE»∆∆Ω√ʃ⁄ƒ≥“ªµ„–˝◊™180°„µ√µΩ°˜PMN£¨Àµ√˜¡ÀPM’˝∫√∫Õx÷·∆Ω––£¨«“PM£ΩOB£Ω1£¨À˘“‘«ÛM°¢Nµƒ◊¯±Íπÿº¸ ««Û≥ˆµ„Mµƒ◊¯±Í£ª ◊œ»∏˘æ𢟵ƒ∫Ø ˝Ω‚Œˆ Ω…Ë≥ˆMµ„µƒ◊¯±Í£¨»ª∫Û∏˘æðÂ∏…Ãıº˛£∫BF£Ω2MF◊˜Œ™µ»¡øπÿœµΩ¯––Ω‚¥º¥ø…£Æ
¢€…Ë°—Q”Î÷±œþCDµƒ«–µ„Œ™G£¨¡¨Ω”QG£¨”…C°¢D¡Ωµ„µƒ◊¯±Í≤ªƒ—≈–∂œ≥ˆ°œCDQ£Ω45°„£¨ƒ«√¥°˜QGDŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨º¥QD £Ω2QG £Ω2QB £¨…Ë≥ˆµ„Qµƒ◊¯±Í£¨»ª∫Û”√Qµ„◊ð◊¯±Í±Ì¥Ô≥ˆQD°¢QBµƒ≥§£¨∏˘æð…œ√ʵƒµ» Ω¡–∑Ω≥ú¥ø…«Û≥ˆµ„Qµƒ◊¯±Í£Æ
œÍΩ‚:
£®1£©°þy=ax2©Å2ax©Å3a=a£®x©Å1£©2©Å4a£¨
°ýD£®1£¨©Å4a£©£Æ
£®2£©¢Ÿ°þ“‘ADŒ™÷±æ∂µƒ‘≤æ≠π˝µ„C£¨
°ý°˜ACDŒ™÷±Ω«»˝Ω«–Œ£¨«“°œACD=90°„£ª
”…y=ax2©Å2ax©Å3a=a£®x©Å3£©£®x+1£©÷™£¨A£®3£¨0£©°¢B£®©Å1£¨0£©°¢C£®0£¨©Å3a£©£¨‘Ú£∫
AC2=9a2+9°¢CD2=a2+1°¢AD2=16a2+4
”…π¥π…∂®¿Ìµ√£∫AC2+CD2=AD2£¨º¥£∫9a2+9+a2+1=16a2+4£¨
ªØºÚ£¨µ√£∫a2=1£¨”…a£º0£¨µ√£∫a=©Å1£¨
¢⁄°þa=©Å1£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ Ω£∫y=©Åx2+2x+3£¨D£®1£¨4£©£Æ
°þΩ´°˜OBE»∆∆Ω√ʃ⁄ƒ≥“ªµ„–˝◊™180°„µ√µΩ°˜PMN£¨
°ýPM°Œx÷·£¨«“PM=OB=1£ª
…ËM£®x£¨©Åx2+2x+3£©£¨‘ÚOF=x£¨MF=©Åx2+2x+3£¨BF=OF+OB=x+1£ª
°þBF=2MF£¨
°ýx+1=2£®©Åx2+2x+3£©£¨ªØºÚ£¨µ√£∫2x2©Å3x©Å5=0
Ω‚µ√£∫x1=©Å1£®…·»•£©°¢x2=![]() .
.
°ýM£®![]() £¨
£¨![]() £©°¢N£®
£©°¢N£®![]() £¨
£¨![]() £©£Æ
£©£Æ
¢€…Ë°—Q”Î÷±œþCDµƒ«–µ„Œ™G£¨¡¨Ω”QG£¨π˝C◊˜CH°ÕQD”⁄H£¨»Áœ¬Õº£∫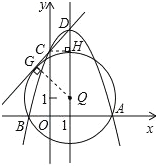
°þC£®0£¨3£©°¢D£®1£¨4£©£¨
°ýCH=DH=1£¨º¥°˜CHD «µ»—¸÷±Ω«»˝Ω«–Œ£¨
°ý°˜QGD“≤ «µ»—¸÷±Ω«»˝Ω«–Œ£¨º¥£∫QD2=2QG2£ª
…ËQ£®1£¨b£©£¨‘ÚQD=4©Åb£¨QG2=QB2=b2+4£ª
µ√£∫£®4©Åb£©2=2£®b2+4£©£¨
ªØºÚ£¨µ√£∫b2+8b©Å8=0£¨Ω‚µ√£∫b=©Å4°¿2![]() £ª
£ª
º¥µ„Qµƒ◊¯±ÍŒ™£®1£¨![]() £©ªÚ£®1£¨
£©ªÚ£®1£¨![]() £©£Æ
£©£Æ

 ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏
ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏ –°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
–°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏