题目内容
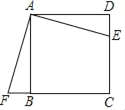
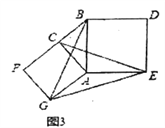
【题目】如图，在矩形ABCD中，AB=m（m是大于0的常数），BC=8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE=x，BF=y．
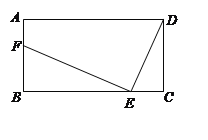
（1）求y关于x的函数关系式；
（2）若m=8，求x为何值时，y的值最大，最大值是多少？
（3）若
，要使△DEF为等腰三角形，m的值应为多少？
【答案】（1）
，（2）当
=4时， 
的值最大，最大值是2，（3）6或2
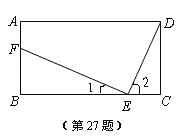
【解析】⑴在矩形ABCD中，∠B=∠C=Rt∠，
∴在Rt△BFE中， ∠1+∠BFE=90°，
又∵EF⊥DE ∴∠1+∠2=90°，
∴∠2=∠BFE，
∴Rt△BFE∽Rt△CED
∴
即
∴
⑵当
=8时， 
，化成顶点式: 
，
∴当
=4时， 
的值最大，最大值是2.
⑶由
，及
得
的方程: 
，得， 
，
∵△DEF中∠FED是直角，
∴要使△DEF是等腰三角形，则只能是EF=ED，
此时， Rt△BFE≌Rt△CED，
∴当EC=2时， 
=CD=BE=6;
当EC=6时， 
=CD=BE=2.
即
的值应为6或2时， △DEF是等腰三角形.
练习册系列答案
名校课堂系列答案
相关题目
