��Ŀ����
����Ŀ����ͼ1�����ǰѶԽ����ഹֱ���ı��ν��������ı��Σ�

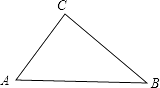
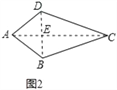
(l)�������⣺��ͼ2�����ı���ABCD�У�AB=AD��CB=CD�����ı���ABCD�Ǵ����ı�������˵�����ɣ�
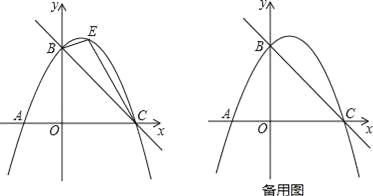
(2)����̽峣���̽�������ı���ABCD����Ա�AB��CD��BC��AD֮���������ϵ��
�������:��Ҫ������������������
д��֤�����̣��Ȼ���ͼ�Σ�д����֪����֤��
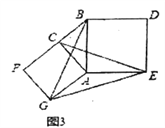
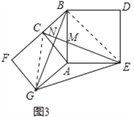
(3)����������ͼ3���ֱ���Rt��ACB��ֱ�DZ�AC��б��ABΪ��������������ACFG��������ABDE������CE��BG��GE����֪AC=4��AB=5,��GE����
���𰸡���1���ı���ABCD�Ǵ����ı���,���ɼ�����;��2��������ۣ������ı��ε�����Աߵ�ƽ�������,���̼�����;��3��GE=![]()
�������������������1�����ݴ�ֱƽ���ߵ��ж������ɵã�ֱ��AC���߶�BD�Ĵ�ֱƽ���ߣ����۵�֤��
��2�����ݴ�ֱ�Ķ���ɵá�AED=��AEB=��BEC=��CED=90�����ɹ��ɶ�����AD2+BC2=AE2+DE2+BE2+CE2�������õ��𰸣�
��3������CG��BE������������GAB�ա�CAE����֪��ABG=��AEC�������õ��ı���BCGE�Ǵ����ı��Σ����������ݴ����ı��ε����ʡ����ɶ����Լ���2���Ľ��۽��м�����⣬������ɽ��.
���������
�⣺��1���ı���ABCD�Ǵ����ı��Σ�
֤������AB=AD��
���A���߶�BD�Ĵ�ֱƽ�����ϣ�
��CB=CD��
���C���߶�BD�Ĵ�ֱƽ�����ϣ�
��ֱ��AC���߶�BD�Ĵ�ֱƽ���ߣ�
��AC��BD�����ı���ABCD�Ǵ����ı��Σ�
��2��������ۣ������ı��ε�����Աߵ�ƽ������ȣ�
��ͼ2����֪�ı���ABCD�У�AC��BD������ΪE��
��֤��AD2+BC2=AB2+CD2
֤������AC��BD��
���AED=��AEB=��BEC=��CED=90����
�ɹ��ɶ����ã�AD2+BC2=AE2+DE2+BE2+CE2��
AB2+CD2=AE2+BE2+CE2+DE2��
��AD2+BC2=AB2+CD2��
��3������CG��BE��
�ߡ�CAG=��BAE=90����
���CAG+��BAC=��BAE+��BAC������GAB=��CAE��
�ڡ�GAB�͡�CAE�У�
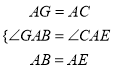 ��
��
���GAB�ա�CAE��
���ABG=��AEC���֡�AEC+��AME=90����
���ABG+��AME=90������CE��BG��
���ı���CGEB�Ǵ����ı��Σ�
�ɣ�2���ã�CG2+BE2=CB2+GE2��
��AC=4��AB=5��
��BC=3��CG=4![]() ��BE=5
��BE=5![]() ��
��
��GE2=CG2+BE2��CB2=73��
��GE=![]() ��
��