题目内容
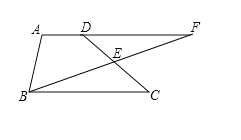
【题目】如图,![]() 和
和![]() 是
是![]() 分别沿着边AB、AC翻折180°形成的.DC的延长线交AE于点O,交BE的延长线于点F.若
分别沿着边AB、AC翻折180°形成的.DC的延长线交AE于点O,交BE的延长线于点F.若![]() ,,则
,,则![]() 的度数为_______.
的度数为_______.
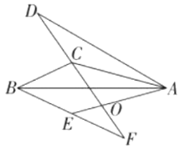
【答案】30°
【解析】
根据∠BCA:∠ABC:∠BAC=28: 5: 3,三角形的内角和定理分别求得∠BCA,∠ABC,
∠BAC的度数,然后根据折叠的性质求出∠D、∠DAE、∠BEA的度数,在△AOD中,根据三角形的内角和定理求出∠AOD的度数,继而可求得∠EOF的度数,最后根据三角形的外角定理求出∠EFC的度数.
∵∠BCA:∠ABC:∠BAC=28:5:3,
∴设∠BCA为28x,∠ABC为5x,∠BAC为3x,
则28x+5x+3x=180°,
解得:x=5°,
则∠BCA=140°,∠ABC=25°,∠BAC=15°,
由折叠的性质可得:∠D=25°,∠DAE=3∠BAC=45°,∠BEA=140°,
在△AOD中,∠AOD=180°-∠DAE-∠D=110°,
∴∠EOF=∠AOD=110°,
∴∠EFC=∠BEA-∠EOF=140°-110°=30°.

练习册系列答案
相关题目