题目内容
【题目】如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.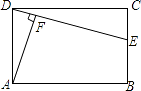
(1)求证:DFCD=AFCE.
(2)若AF=4DF,CD=12,求CE的长.
【答案】
(1)证明:
∵四边形ABCD是矩形,
∴∠ADC=∠C=90°,
∴∠ADF+∠CDE=90°,
∵AF⊥DE,
∴∠AFD=∠DAF+∠FDA=90°,
∴∠FAD=∠CDE,
又∵∠C=∠AFD=90°,
∴△ADF∽△DCE;
∴ ![]() ,
,
即DFCD=AFCE
(2)解:∵△ADF∽△DCE;
∴ ![]() ,
,
∴ ![]()
![]() ,
,
又∵AF=4DF,CD=12,
∴ ![]() ,
,
∴CE=3.
【解析】(1)根据矩形的性质得出∠ADC=∠C=90°,根据同角的余角相等得出∠FAD=∠CDE,进而判断出△ADF∽△DCE;根据相似三角形对应边成比例得出结论;
(2)根据根据相似三角形对应边成比例得出![]() =
=![]() ,根据比例的性质得出
,根据比例的性质得出![]() =
=![]() ,将AF=4DF,CD=12,代入即可求出CE的长。
,将AF=4DF,CD=12,代入即可求出CE的长。
【考点精析】本题主要考查了矩形的性质和比例的性质的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;基本性质;更比性质(交换比例的内项或外项);反比性质(交换比的前项、后项);等比性质才能正确解答此题.

练习册系列答案
相关题目