Question

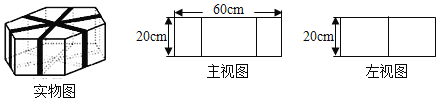
【题目】如图，上、下底面为全等的正六边形礼盒，其主视图与左视图均由矩形构成，主视图中大矩形边长如图，左视图中包含两个全等的矩形，如果用彩色胶带按如图包扎礼盒，所需胶带长度至少为___________ cm.(精确到0.001 cm)

Answer 1

【答案】431.769

【解析】

由主视图知道，高是20cm，两顶点之间的最大距离为60cm，应利用正六边形的性质求得底面对边之间的距离，然后所有棱长相加即可．

根据题意，作出实际图形的上底，

如图：AC，CD是上底面的两边．

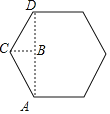
则AC=60÷2=30（cm），∠ACD=120°，

作CB⊥AD于点B，

那么AB=AC×sin60°=15（cm），

所以AD=2AB=30（cm），

胶带的长至少=30×6+20×6≈431.769（cm）．

故答案为：431.769．