题目内容
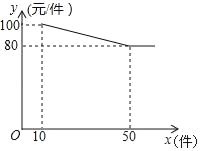
【题目】服装厂批发某种服装,每件成本为65元,规定不低于10件可以批发,其批发价y(元/件)与批发数量x(件)(x为正整数)之间所满足的函数关系如图所示.
(1)求y与x之间所满足的函数关系式,并写出x的取值范围;
(2)设服装厂所获利润为w(元),若10≤x≤50(x为正整数),求批发该种服装多少件时,服装厂获得利润最大?最大利润是多少元?
【答案】(1)y=![]() (2)批发该种服装40件时,服装厂获得利润最大,最大利润是800元
(2)批发该种服装40件时,服装厂获得利润最大,最大利润是800元
【解析】
(1)认真观察图象,分别写出该定义域下的函数关系式,定义域取值全部是整数;
(2)根据利润=(售价-成本)×件数,列出利润的表达式,求出最值.
(1)当10≤x≤50时,设y与x的函数关系式为y=kx+b,
![]() ,得
,得![]() ,
,
∴当10≤x≤50时,y与x的函数关系式为y=﹣0.5x+105,
当x>50时,y=80,
即y与x的函数关系式为:y=![]() ;
;
(2)由题意可得,
w=(﹣0.5x+105﹣65)x=﹣0.5x2+40x=﹣0.5(x﹣40)2+800,
∴当x=40时,w取得最大值,此时w=800,y=﹣0.5×40+105=85,
答:批发该种服装40件时,服装厂获得利润最大,最大利润是800元.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
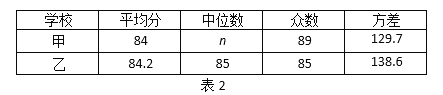
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.