题目内容
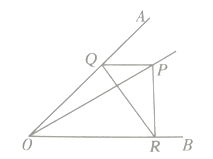
【题目】如图，
是
内的一点，
，点
分别在的两边上，
周长的最小值是____．
【答案】
【解析】
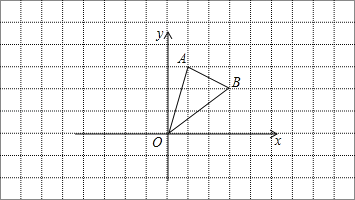
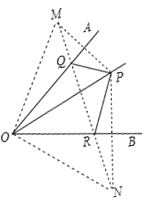
根据轴对称图形的性质，作出P关于OA、OB的对称点M、N，连接OM、ON、MN，根据两点之间线段最短得到MN即为△PQR周长的最小值，然后证明△MON为等腰直角三角形，利用勾股定理求出MN即可．
解：分别作P关于OA、OB的对称点M、N，连接OM、ON，连接MN交OA、OB交于Q、R，则△PQR符合条件且△PQR的周长等于MN，
由轴对称的性质可得：OM＝ON＝OP＝10，∠MOA＝∠POA，∠NOB＝∠POB，
∴∠MON＝∠MOP＋∠NOP＝2∠AOB＝90°，
∴△MON为等腰直角三角形．
∴MN＝
，
所以△PQR周长的最小值为，
故答案为：．
练习册系列答案
中考解读考点精练系列答案
相关题目
【题目】为了加强学生的安全意识，某校组织了学生参加安全知识竞赛，从中抽取了部分的学生成绩进行统计，绘制统计图如图（不完整）．
类别 | 分数段 |
A | 50.5～60.5 |
B | 60.5～70.5 |
C | 70.5～80.5 |
D | 80.5～90.5 |
E | 90.5～100.5 |
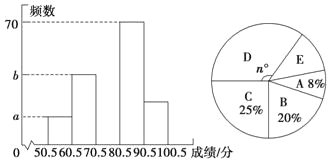
请你根据上面的信息，解答下列问题．
（1）若A组的频数比B组小24，求频数直方图中的a，b的值；
（2）在扇形统计图中，D部分所对的圆心角为n°，求n的值并补全频数直方图；
（3）若成绩在80分以上为优秀，全校共有2 000名学生，估计成绩优秀的学生有多少名？
