��Ŀ����
����Ŀ������ˮ��ɽ�����ǽ�ɽ��ɽ����ij���ξ���Ϊ�˱����������蹺��ף��������ͺŵ����������豸��10̨����֪ÿ̨�����豸�մ�������Ϊ12�֣�ÿ̨�����豸�մ�������Ϊ15�֣����ص��豸�մ��������ܼƲ�����140�֣�
��1������Ϊ�þ�����ƹ���ף��������豸�ķ�����
��2����֪ÿ̨�����豸�۸�Ϊ3��Ԫ��ÿ̨�����豸�۸�Ϊ4��4��Ԫ������Ϊ�˴�����Ʒ���涨�ܻ������40��Ԫʱ���ɰ�9���Żݣ��ʲ��ã�1������Ƶ����ֹ�����ʹ����������٣�
���𰸡���1������һ����������豸1̨�������豸9̨������������������豸2̨�������豸8̨������������������豸3̨�������豸7̨����2�����ã�1����Ƶĵڶ��ַ�����ʹ����������٣�
��������
��1���蹺������豸x̨�����������豸��10-x��̨�����ݹ��ص��豸�մ�������������140���г�����ʽ12x+15��10-x����140������⼯���ٸ���xΪ���������ó�x=1��2��3��������⼴�ɣ�
��2���ֱ����������ʵ�ʹ�����ã��Ƚϼ�����⣮
��1���蹺������豸x̨�����������豸��10-x��̨��
�������⣬��12x+15��10-x����140��
���x��3![]() ��
��
��x��������
��x=1��2��3��
��þ�����������Ʒ�����
����һ����������豸1̨�������豸9̨��
����������������豸2̨�������豸8̨��
����������������豸3̨�������豸7̨��
��2��������������÷ֱ�Ϊ��
����һ��3��1+4.4��9=42.6��40��ʵ�ʸ��42.6��0.9=38.34����Ԫ����
��������3��2+4.4��8=41.2��40��ʵ�ʸ��41.2��0.9=37.08����Ԫ����
��������3��3+4.4��7=39.8��40��ʵ�ʸ��39.8����Ԫ����
��37.08��38.34��39.8��
����ã�1����Ƶĵڶ��ַ�����ʹ����������٣�

����Ŀ��Ϊ�˼�ǿѧ���İ�ȫ��ʶ��ijУ��֯��ѧ���μӰ�ȫ֪ʶ���������г�ȡ�˲��ֵ�ѧ���ɼ�����ͳ�ƣ�����ͳ��ͼ��ͼ������������
��� | ������ |
A | 50.5��60.5 |
B | 60.5��70.5 |
C | 70.5��80.5 |
D | 80.5��90.5 |
E | 90.5��100.5 |
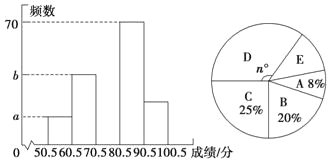
��������������Ϣ������������⣮
��1����A���Ƶ����B��С24����Ƶ��ֱ��ͼ�е�a��b��ֵ��
��2��������ͳ��ͼ�У�D�������Ե�Բ�Ľ�Ϊn�㣬��n��ֵ����ȫƵ��ֱ��ͼ��
��3�����ɼ���80������Ϊ���㣬ȫУ����2 000��ѧ�������Ƴɼ������ѧ���ж�������