题目内容
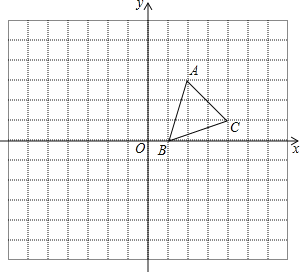
【题目】如图,已知抛物线过点A(4,0),B(﹣2,0),C(0,﹣4).
(1)求抛物线的解析式;
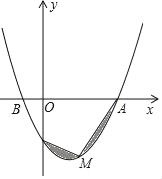
(2)如图,点M是抛物线AC段上的一个动点,当图中阴影部分的面积最小值时,求点M的坐标.
【答案】(1)y=![]() x2﹣x﹣4(2)当x=2时,△ACM的面积最大,图中阴影部分的面积最小值,此时M点坐标为(2,﹣4)
x2﹣x﹣4(2)当x=2时,△ACM的面积最大,图中阴影部分的面积最小值,此时M点坐标为(2,﹣4)
【解析】
根据A、B点的坐标特点设函数解析式为y=a(x+2)(x﹣4),然后将C点坐标代入即可求;
连接AC,设M点坐标为(x,![]() x2﹣x﹣4),利用x表示出S△ACM,然后转化成函数解析式即可求解.
x2﹣x﹣4),利用x表示出S△ACM,然后转化成函数解析式即可求解.
(1)设抛物线解析式为y=a(x+2)(x﹣4),
把C(0,﹣4)代入得a2(﹣4)=﹣4,
解得a=![]() ,
,
∴抛物线解析式为y=![]() (x+2)(x﹣4),
(x+2)(x﹣4),
即y=![]() x2﹣x﹣4;
x2﹣x﹣4;
(2)连接AC,则AC与抛物线所围成的图形的面积为定值,
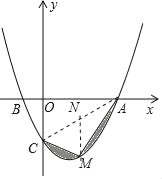
当△ACM的面积最大时,图中阴影部分的面积最小值,
作MN∥y轴交AC于N,如图甲,
设M(x,![]() x2﹣x﹣4),
x2﹣x﹣4),
由A(4,0),C(0,﹣4)知线段AC所在直线解析式为y=x﹣4,
则N(x,x﹣4),
∴MN=x﹣4﹣(![]() x2﹣x﹣4)=﹣
x2﹣x﹣4)=﹣![]() x2+2x,
x2+2x,
∴S△ACM=S△MNC+S△MNA=![]() 4MN=﹣x2+4x=﹣(x﹣2)2+4,
4MN=﹣x2+4x=﹣(x﹣2)2+4,
当x=2时,△ACM的面积最大,图中阴影部分的面积最小值,
此时M点坐标为(2,﹣4).

练习册系列答案
相关题目