题目内容
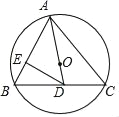
【题目】如图,在中⊙O,AB 是直径,弦 AE 的垂直平分线交⊙O 于点 C,CD⊥AB于 D,BD=1,AE=4,则 AD 的长为___.
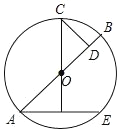
【答案】4
【解析】
证明△AOF≌△COD(AAS),得 CD=AF=2,设⊙O 的半径为 r,则 OD=r﹣1,根据勾股定理列方程可得结论.
如图:
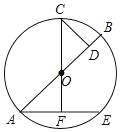
弦AE的垂直平分线交⊙O于点 F,
∴AF= ![]() AE=2,∠AFO=90°,
AE=2,∠AFO=90°,
∵CD⊥AB,
∴∠ODC=∠AFO=90°,
∵OA=OC,∠AOF=∠COD,
∴△AOF≌△COD(AAS),
∴CD=AF=2,
设⊙O的半径为 r,则 OD=r﹣1, 由勾股定理得:OC2=OD2+CD2, r2=(r﹣1)2+22,
r=![]() ,
,
∴AD=AB﹣1=2× ![]() ﹣1=4,
﹣1=4,
故答案为:4.

练习册系列答案
相关题目
【题目】⊙O 的直径 AB 长为 10,弦 MN⊥AB,将⊙O 沿 MN 翻折,翻折后点 B 的对应点为点 B′,若 AB′=2,MB′的长为( )
A. 2 ![]() B. 2
B. 2![]() 或 2
或 2![]() C. 2
C. 2![]() D. 2
D. 2 ![]() 或 2
或 2![]()
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.