Question

【题目】阅读理解题．

定义：如果四边形的某条对角线平分一组对角，那么把这条对角线叫做“美妙线”，该四边形叫做“美妙四边形”．

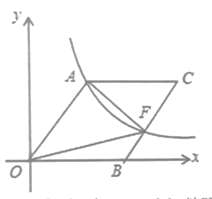
如图，在四边形ABDC中，对角线BC平分∠ACD和∠ABD，那么对角线BC叫“美妙线”，四边形ABDC就称为“美妙四边形”．

问题：

（1）下列四边形：平行四边形、矩形、菱形、正方形，其中是“美妙四边形”的有 个；

（2）四边形ABCD是“美妙四边形”，AB=∠BAD=60°，∠ABC=90°，求四边形ABCD的面积．（画出图形并写出解答过程）

Answer 1

【答案】（1）2 ；（2）或．

【解析】

（1）由四边形的性质可知：菱形和正方形的每条对角线平分一组对角结合“美妙四边形”的定义即可确定；

（2）分AC或BD是美妙线两种情况，先证明△ABC≌△ADC，则S四边形ABCD=2S△ABC,最后代入即可．

解：（1）∵菱形和正方形的每一条对角线平分一组对角，

∴菱形和正方形是“美妙四边形”.

故答案为2；

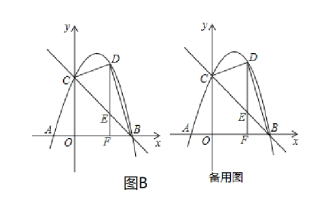
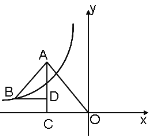
(2) ① 当AC为“美妙线”时，如图：

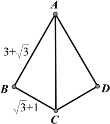
易得，即

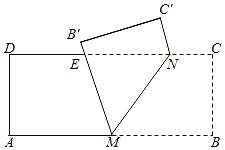
②若BD为“美妙线”，如图：作DE⊥AB于点E

设AE=x，则DE=x，BE=x

∴

∴

∴，即

综上，四边形的面积为或．