题目内容
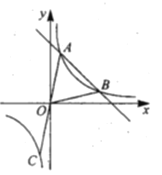
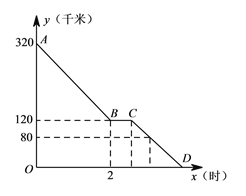
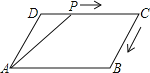
【题目】如图，在平行四边形ABCD中，∠DAB=60°，AB=5，BC=3,点P从点D出发，沿DC,CB向终点B匀速运动．设点P所走过的路程为x，点P所经过的线段与AD,AP所围成的图形的面积为y,y随x的变化而变化．在下列图象中，能正确反映y与x的函数关系的是（ ）
A.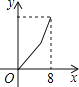
B.
C.
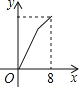D.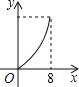
【答案】A
【解析】
本题考查动点函数图象的问题，先求出函数关系式在判断选项．
∵四边形ABCD是平行四边形，
∴AD=BC=3，AB=CD=5
当点P在CD上运动时，y为三角形，面积为：
×DP×ADsin60°=×3×sin60°=×3×
x＝
x，为正比例函数；
当点P在CB上运动时，y为梯形，面积为：×(AD+CP)×ABsin60°=×（3+x5）×
5× ＝
，为一次函数．
由于后面的面积的x的系数＞前面的x的系数，所以后面函数的图象应比前面函数图象要陡．
故选：A．
练习册系列答案
相关题目
