题目内容
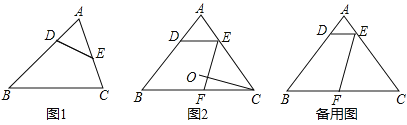
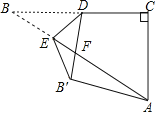
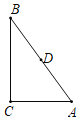
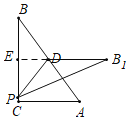
【题目】如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点D是AB的中点，点P是直线BC上一点，将△BDP沿DP所在的直线翻折后，点B落在B1处，若B1D⊥BC，则点P与点B之间的距离为（ ）
A.1B.
C.1或 3D.或5
【答案】D
【解析】
分点B1在BC左侧，点B1在BC右侧两种情况讨论，由勾股定理可AB=5，由平行线分线段成比例可得
，可求BE，DE的长，由勾股定理可求PB的长．
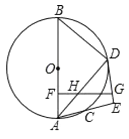
解：如图，若点B1在BC左侧，
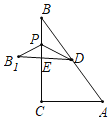
∵∠C=90°，AC=3，BC=4，
∴AB=
∵点D是AB的中点，
∴BD=
BA=
∵B1D⊥BC，∠C=90°
∴B1D∥AC
∴
∴BE=EC=BC=2，DE=AC=
∵折叠
∴B1D=BD=，B1P=BP
∴B1E=B1D-DE=1
∴在Rt△B1PE中，B1P2=B1E2+PE2，
∴BP2=1+（2-BP）2，
∴BP=
如图，若点B1在BC右侧，
∵B1E=DE+B1D=+，
∴B1E=4
在Rt△EB1P中，B1P2=B1E2+EP2，
∴BP2=16+（BP-2）2，
∴BP=5
故选：D．
练习册系列答案
相关题目
【题目】某工厂对一批灯泡的质量进行随机抽查，见下表：
抽取灯泡数 | 40 | 100 | 150 | 500 | 1000 | 1500 |
优等品数 | 36 | 92 | 145 | 474 | 950 | 1427 |
优等品频率 |
（1）计算表中的优等品的频率（精确到0.001）
（2）根据抽査的灯泡优等品的频率，估计这批灯泡优等品的概率（精确到0.01）
