Question

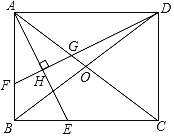
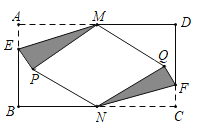
【题目】如图，有一张矩形纸条ABCD，AB＝5cm，BC＝2cm，点M，N分别在边AB，CD上，CN＝1cm．现将四边形BCNM沿MN折叠，使点B，C分别落在点B'，C'上．当点B'恰好落在边CD上时，线段BM的长为_____cm；在点M从点A运动到点B的过程中，若边MB'与边CD交于点E，则点E相应运动的路径长为_____cm．

Answer 1

【答案】

【解析】

第一个问题证明BM＝MB′＝NB′，求出NB即可解决问题．第二个问题，探究点E的运动轨迹，寻找特殊位置解决问题即可．

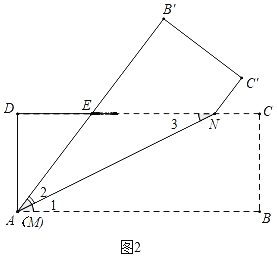
如图1中，

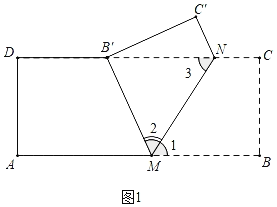
∵四边形ABCD是矩形，

∴AB∥CD，

∴∠1＝∠3，

由翻折的性质可知：∠1＝∠2，BM＝MB′，

∴∠2＝∠3，

∴MB′＝NB′，

∵NB′＝＝＝（cm），

∴BM＝NB′＝（cm）．

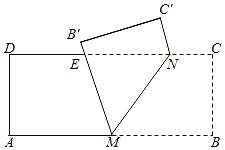
如图2中，当点M与A重合时，AE＝EN，设AE＝EN＝xcm，

在Rt△ADE中，则有x2＝22+（4﹣x）2，解得x＝，

∴DE＝4﹣＝（cm），

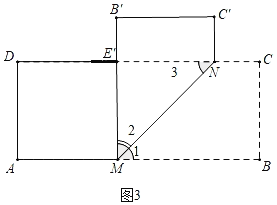
如图3中，当点M运动到MB′⊥AB时，DE′的值最大，DE′＝5﹣1﹣2＝2（cm），

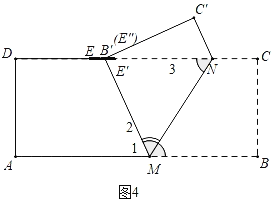
如图4中，当点M运动到点B′落在CD时，DB′（即DE″）＝5﹣1﹣＝（4﹣）（cm），

∴点E的运动轨迹E→E′→E″，运动路径＝EE′+E′B′＝2﹣+2﹣（4﹣）＝（）（cm）．

故答案为，（）．