题目内容
【题目】正方形![]() 的边长为
的边长为![]() ,在各边上顺次截取
,在各边上顺次截取![]() ,则边形
,则边形![]() 是________,面积为________.
是________,面积为________.
【答案】正方形 ![]()
【解析】
由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出四边形EFGH是正方形,由勾股定理得EH,即可得出正方形EFGH的面积.
如图所示:
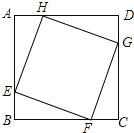
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,
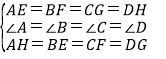 ,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH=![]() ,
,
∴四边形EFGH的面积=EH2=34,
故答案是:正方形,34.

练习册系列答案
相关题目







