��Ŀ����
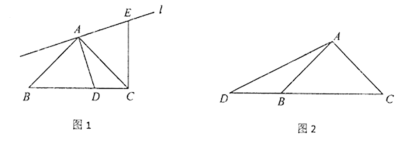
����Ŀ����ͼ������ABCD�ı߳�Ϊ20cm����ABC=120�����Խ���AC��BD�ཻ�ڵ�O������P�ӵ�A��������4cm/s���ٶȣ���A��B��·�����B�˶�������P��PQ��BD����AC�ཻ�ڵ�Q�����˶�ʱ��Ϊt�룬0��t��5��

��1�����ı���PQCB�����ΪS����S��t�Ĺ�ϵʽ��
��2������Q����O�ĶԳƵ�ΪM������P�Ҵ�ֱ��AB��ֱ��l������ABCD�ı�AD����CD���ڵ�N����tΪ��ֵʱ����P��M��N��һֱ���ϣ�
��3��ֱ��PN��AC�ཻ��H�㣬����PM��NM���Ƿ����ijһʱ��t��ʹ��ֱ��PNƽ���ı���APMN������������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1) S=��2![]() ��0��t��5���� (2)
��0��t��5���� (2) ![]() ;(3)������.
;(3)������.
��������
��1����ͼ1������S=S��ABC-S��APQ������ɵ�S��t�Ĺ�ϵʽ��
��2����PM=x����AM=2x���ɵ�AP=![]() x=4t������x��ֵ������ֱ��������30�Ƚǵ����ʿɵ�AM=2PM=
x=4t������x��ֵ������ֱ��������30�Ƚǵ����ʿɵ�AM=2PM=![]() ������AM=AO+OM���з��̿ɵ�t��ֵ��
������AM=AO+OM���з��̿ɵ�t��ֵ��
��3�����ڣ�ͨ����ͼ��֪��N��CD��ʱ��ֱ��PNƽ���ı���APMN����������������ȿɵ�MG=AP����AM=AO+OM����ʽ�ɵ�t��ֵ��
�⣺��1����ͼ1�����ı���ABCD�����Σ�
���ABD=��DBC=![]() ��ABC=60�㣬AC��BD��
��ABC=60�㣬AC��BD��
���OAB=30�㣬
��AB=20��
��OB=10��AO=10![]() ��
��
������ã�AP=4t��
��PQ=2t��AQ=2![]() t��
t��
��S=S��ABC��S��APQ��
=![]() ��
��
=![]() ��
��
=��2![]() t2+100
t2+100![]() ��0��t��5����
��0��t��5����
��2����ͼ2����Rt��APM�У�AP=4t��
�ߵ�Q����O�ĶԳƵ�ΪM��
��OM=OQ��
��PM=x����AM=2x��
��AP=![]() x=4t��
x=4t��
��x=![]() ��
��
��AM=2PM=![]() ��
��
��AM=AO+OM��
��![]() =10
=10![]() +10
+10![]() ��2
��2![]() t��
t��
t=![]() ��
��
�𣺵�tΪ![]() ��ʱ����P��M��N��һֱ���ϣ�
��ʱ����P��M��N��һֱ���ϣ�
��3�����ڣ�
��ͼ3����ֱ��PNƽ���ı���APMN�������
��S��APN=S��PMN��
��M��MG��PN��G��
�� ![]() ��
��
��MG=AP��
�á�APH�ա�MGH��
��AH=HM=![]() t��
t��
��AM=AO+OM��
ͬ����֪��OM=OQ=10![]() ��2
��2![]() t��
t��
![]() t=10
t=10![]() =10
=10![]() ��2
��2![]() t��
t��
t=![]() ��
��
�𣺵�tΪ![]() ��ʱ��ʹ��ֱ��PNƽ���ı���APMN�������
��ʱ��ʹ��ֱ��PNƽ���ı���APMN�������

����Ŀ����֪���κ���![]() ��
��![]() ��
��![]() �IJ�����Ӧֵ���±���
�IJ�����Ӧֵ���±���
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�ҷ���![]() �������ֱ�Ϊ
�������ֱ�Ϊ![]() ��
��![]()
![]() ������˵��������ǣ� ����
������˵��������ǣ� ����
A. ![]() ��
��![]() B.
B. ![]()
C. ��![]() ʱ��
ʱ��![]() D. ��
D. ��![]() ʱ��
ʱ��![]() ����Сֵ
����Сֵ