题目内容
如图，已知AB是⊙O的直径，BC是和⊙O相切于点B的切线，⊙O的弦AD平行于OC，若OA=2，且AD+OC=6，则CD=______．
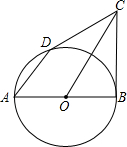
连接BD，则∠ADB=90°；
∵AD∥OC，
∴OC⊥BD；
根据垂径定理，得OC是BD的垂直平分线，即CD=BC；
延长AD交BC的延长线于E；
∵O是AB的中点，且AD∥OC；
∴OC是△ABE的中位线；
设OC=x，则AD=6-x，AE=2x，DE=3x-6；
Rt△ABE中，根据勾股定理，得：BE2=4x2-16；
由切割线定理，得BE2=ED•AE=2x（3x-6）；
∴4x2-16=2x（3x-6），解得x=2，x=4；
当x=2时，OC=OB=2，由于OC是Rt△OBC的斜边，显然x=2不合题意，舍去；
当x=4时，OC=4，OB=2；
在Rt△OBC中，CB=
=2
．
∴CD=CB=2
．
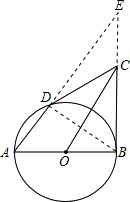
∵AD∥OC，
∴OC⊥BD；
根据垂径定理，得OC是BD的垂直平分线，即CD=BC；
延长AD交BC的延长线于E；
∵O是AB的中点，且AD∥OC；
∴OC是△ABE的中位线；
设OC=x，则AD=6-x，AE=2x，DE=3x-6；
Rt△ABE中，根据勾股定理，得：BE2=4x2-16；
由切割线定理，得BE2=ED•AE=2x（3x-6）；
∴4x2-16=2x（3x-6），解得x=2，x=4；
当x=2时，OC=OB=2，由于OC是Rt△OBC的斜边，显然x=2不合题意，舍去；
当x=4时，OC=4，OB=2；
在Rt△OBC中，CB=
| OC2-OB2 |
| 3 |
∴CD=CB=2
| 3 |
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
