题目内容
点P是⊙O外一点，PA、PB分别切⊙O于点A、B，∠P=70°，点C是⊙O上的点（不与点A、B重合），则∠ACB等于（ ）
| A．70° | B．55° | C．70°或110° | D．55°或125° |
如图，
∵PA、PB分别切⊙O于点A、B，
∴∠OAP=∠OBP=90°，
∵∠P=70°，
∴∠AOB=110°，
∴∠ACB=55°，
当点C在劣弧AB上，
∵∠AOB=110°，
∴弧ACB的度数为250°，
∴∠ACB=125°．
故选D．
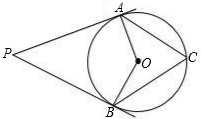
∵PA、PB分别切⊙O于点A、B，
∴∠OAP=∠OBP=90°，
∵∠P=70°，
∴∠AOB=110°，
∴∠ACB=55°，
当点C在劣弧AB上，
∵∠AOB=110°，
∴弧ACB的度数为250°，
∴∠ACB=125°．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
