题目内容
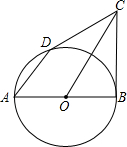
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,过点D作DE⊥AC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)如果BC=8,AB=5,求CE的长.

(1)求证:DE是⊙O的切线;
(2)如果BC=8,AB=5,求CE的长.

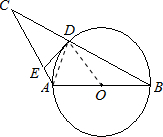
(1)证明:连接OD.
∵OD=OB(⊙O的半径),
∴∠B=∠ODB(等边对等角);
∵AB=AC(已知),
∴∠B=∠C(等边对等角);
∴∠C=∠ODB(等量代换),
∴OD∥AC(同位角相等,两直线平行),
∴∠ODE=∠DEC(两直线平行,内错角相等);
∵DE⊥AC(已知),
∴∠DEC=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线;
(2)连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角);
∴AD⊥CD;
在Rt△ACD和Rt△DCE中,
∠C=∠C(公共角),
∠CED=∠CDA=90°,
∴Rt△ACD∽Rt△DCE(AA),
∴
=
;
又由(1)知,OD∥AC,O是AB的中点,
∴OD是三角形ABC的中位线,
∴CD=
BC;
∵BC=8,AB=5,AB=AC,
∴CE=
.
∵OD=OB(⊙O的半径),
∴∠B=∠ODB(等边对等角);
∵AB=AC(已知),
∴∠B=∠C(等边对等角);
∴∠C=∠ODB(等量代换),
∴OD∥AC(同位角相等,两直线平行),
∴∠ODE=∠DEC(两直线平行,内错角相等);
∵DE⊥AC(已知),
∴∠DEC=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线;
(2)连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角);
∴AD⊥CD;
在Rt△ACD和Rt△DCE中,
∠C=∠C(公共角),
∠CED=∠CDA=90°,
∴Rt△ACD∽Rt△DCE(AA),
∴
| CE |
| CD |
| DC |
| AC |
又由(1)知,OD∥AC,O是AB的中点,
∴OD是三角形ABC的中位线,
∴CD=
| 1 |
| 2 |
∵BC=8,AB=5,AB=AC,
∴CE=
| 16 |
| 5 |


练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
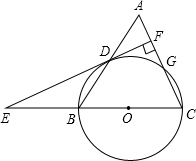

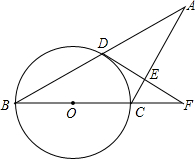 交BC的延长线于点F.
交BC的延长线于点F.