题目内容
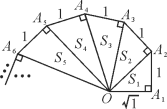
【题目】细心观察图形,认真分析各式,然后解答问题.
OA22=(![]() )2+1=2,S1=
)2+1=2,S1=![]() ;
;
OA32=12+(![]() )2=3,S2=
)2=3,S2=![]() ;
;
OA42=12+(![]() )2=4,S3=
)2=4,S3=![]() ;…
;…
(1)请用含有n(n为正整数)的等式表示上述变化规律:OAn2=________,Sn=________;
(2)若一个三角形的面积是2![]() ,计算说明它是第几个三角形?
,计算说明它是第几个三角形?
(3)求出S12+S22+S32+…+S92的值.
【答案】(1)n, ![]() ;(2)第32个三角形;(3)11.25
;(2)第32个三角形;(3)11.25
【解析】
(1)根据所列式子,找出规律直接写出即可
(2)由于Sn=![]() ,当Sn=
,当Sn=![]() 时,代入求n即可
时,代入求n即可
(3)根据题意直接代入求和即可
(1)n ![]()
(2)当Sn=![]() 时,有
时,有![]() =
=![]() ,解之得n=32,即说明它是第32个三角形
,解之得n=32,即说明它是第32个三角形
(3)S12+S22+S32+…+S92=![]() …
…![]() =
=![]() =11.25
=11.25

练习册系列答案
相关题目
【题目】如图所示的是用棋子成的T字形图案:
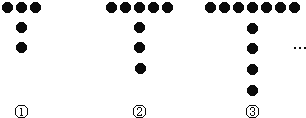
(1)填写下表:
图案序号 | ① | ② | ③ | ④ | …… | ⑧ |
每个图案中棋子的个数 | 5 | 8 | …… |
(2)第![]() 个“T“字形图案中棋子的个数为多少 (用含
个“T“字形图案中棋子的个数为多少 (用含![]() 的代数式表示);
的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.



